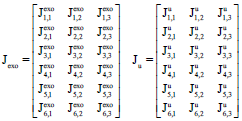
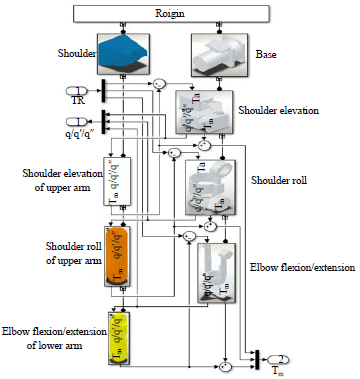
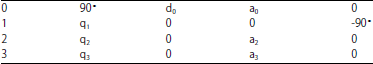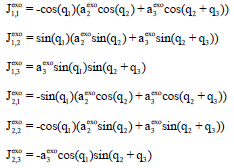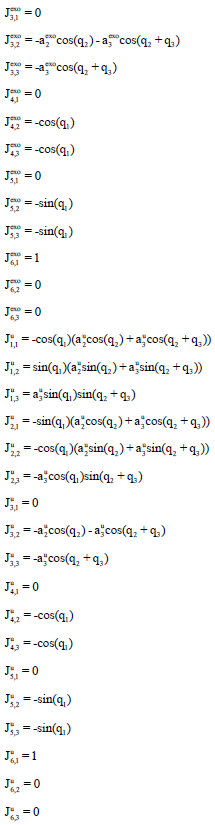Research Article
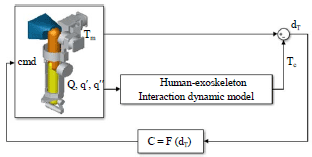
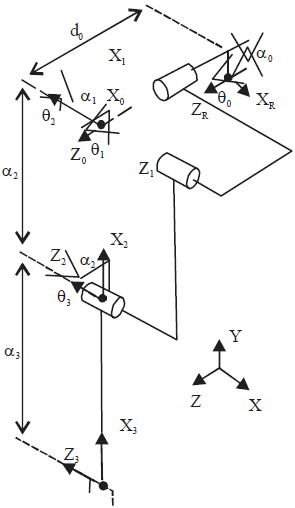
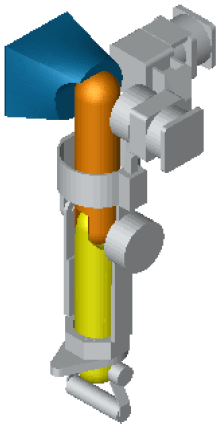
Dynamic Modeling of the Human-Computer Interaction for Upper Limb Rehabilitation Robot
State Key Laboratory of Synthetical Automation for Process Industries, Northeast University, 110004 Shenyang Liaoning Province, China
Xiaofeng Wang
State Key Laboratory of Synthetical Automation for Process Industries, Northeast University, 110004 Shenyang Liaoning Province, China