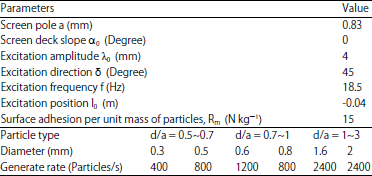
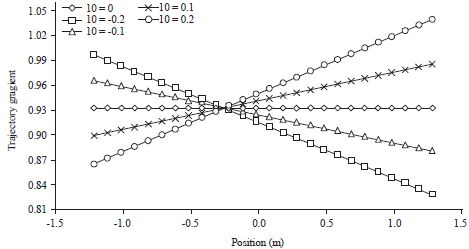
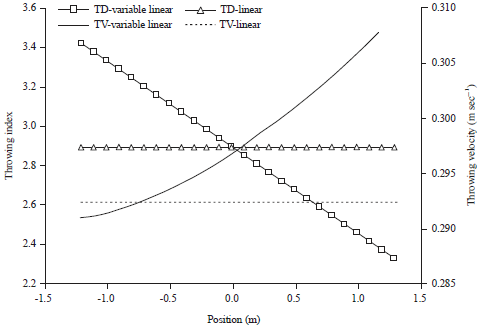
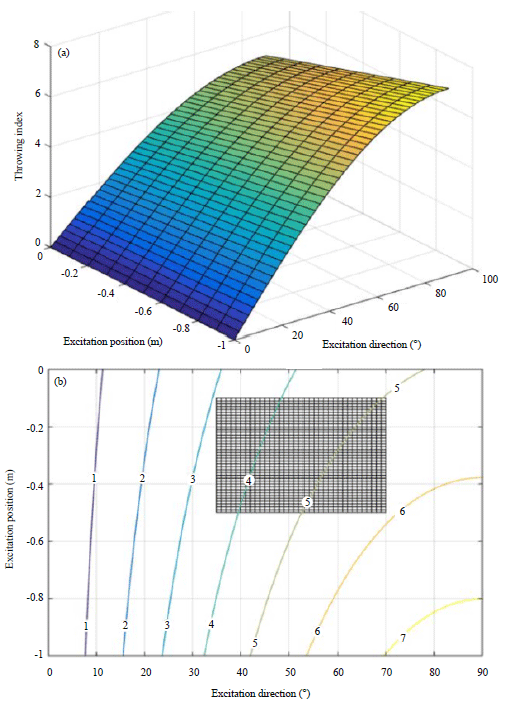
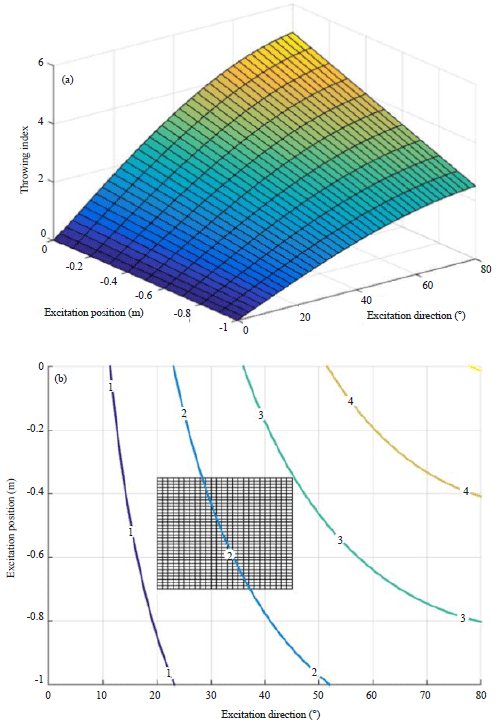
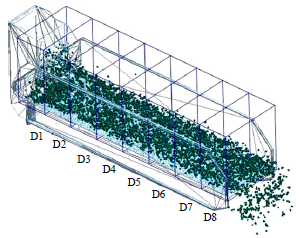
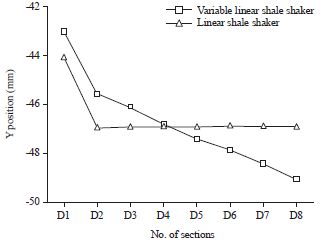
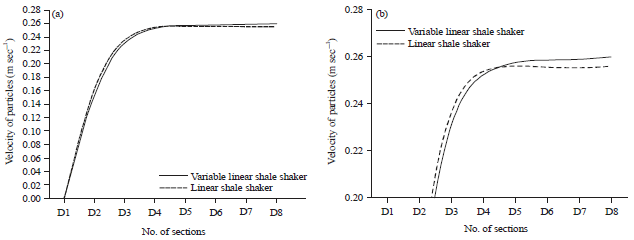
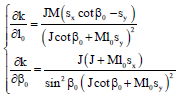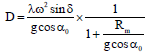Research Article
Dynamical Model and Simulation on Variable Linear Shale Shaker
Institute for Strength and Vibration of Mechanical Structures, Yangtze University, China
Sizhu Zhou
Institute for Strength and Vibration of Mechanical Structures, Yangtze University, China
Zhipeng Lv
Institute for Strength and Vibration of Mechanical Structures, Yangtze University, China
Jian Hua
Institute for Strength and Vibration of Mechanical Structures, Yangtze University, China