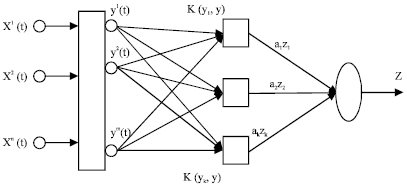
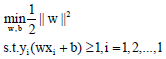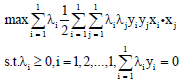Research Article
Arithmetic Based on Wavelet Transform and Process SVM for Automatically Identifying Log-Curve Formation
Northeast Petroleum University, Daqing, 163318, China
Mingtao Wu
Institute of Petroleum Economics and Management, Northeast Petroleum University, Daqing, 163318, China
Jianjun Xu
Northeast Petroleum University, Daqing, 163318, China