ABSTRACT
DV-Hop algorithm is one of the important range-free localization algorithms. It performs better in isotropic density senor networks, however, it brings larger location errors in random distributed networks. According to the localization principle of the DV-Hop algorithm, this study improves the estimation of average single hop distance by using the least equal square error and revises the estimated distance between the unknown node and the anchor node with compensation coefficient considering the wireless sensors deployed in the non-planar application scenarios. This localization algorithm is based on compensation coefficient. Simulation results show that the improved algorithm has better locating performance in locating precision by increasing appropriate computation overhead and is a feasible locating scheme in WSN in both random distributing and dynamic topology networks.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jse.2015.650.657
URL: https://scialert.net/abstract/?doi=jse.2015.650.657
INTRODUCTION
Wireless Sensor Networks (WSN) is composed of a large number of sensor nodes with randomly distributed structure, information collection, processing, self-organizing network forwarding can be done in its cover area. In WSN applications, the location information of the sensor is critical to monitor network activity. In monitoring and tracking the target, routing based on the position information, load balancing of the network, the network topology and other applications (Peng and Wang, 2011), these are required to know the network node own position in advance, the position information is applied in the communication and collaboration process and these applications are completed. Thus, the wireless sensor network positioning technology is the foundation of the entire network, which achieve a variety of functions.
Existing node localization algorithm can be divided into two categories in the different locating ways (Sun et al., 2005), there are algorithm based on the distance (range-based) and algorithm without distance (range-free). In positioning algorithm without ranging, DV-Hop (distance vector-hop) algorithm is one of the typical positioning algorithm, it is one of the distributed localization methods, which are proposed in advantage of distance vector routing and positioning beacon nodes, the method is simple and there is good scalability (Niculescu and Nath, 2001, 2003) but it is the use of jumping distance instead of straight line distance, ideal positioning effect is achieved only in the isotropic dense network.
In this study, because there are the limitations of DV-Hop algorithm in the randomly distributed network environment, the network average value per hop distance is obtained by using minimum mean square error method and the impact on the positioning results are taken into account when monitoring region is non-planar, through the use of compensation coefficient, the fluctuation of the monitored area is reduced, the effects of the calculating distance is defined between the unknown node and beacon node calculation, the positioning accuracy of the algorithm is improved.
METHODOLOGY
DV-Hop localization algorithm: The basic idea of DV-Hop localization algorithm is that the distance between unknown nodes and beacon nodes is equal to the product of the network average distance of the per hop and the hop number between them. When the distance with three or more beacon nodes is obtained on the unknown node, their own positioning can be realized. Its positioning is generally divided into three stages (Sun et al., 2005; Niculescu and Nath, 2001): First the distance vector broadcast protocol is used between nodes and information is forwarded, in all network nodes, the minimum number of hops between each beacon nodes is obtained; secondly, after the position of the other beacon nodes and a minimum hop count are obtained in the beacon node, the average network hop distance is calculated and then it is as a correction is broadcasted to the network. The first correction is only received and record and it is forwarded to the neighbor nodes and then based on the smallest hop records, the hop distance is calculated near each beacon node. Finally, when the distances are obtained from an unknown node to three or more beacon nodes and the trilateration method or maximum likelihood estimation method are performed to calculate their coordinates.
Beacon nodes i, j, k are shown in Fig. 1, the linear distances dij, dik can be calculated between them according to the distance equation. If the minimum number of hops from i to j and k is hopsij and hopsik, the average network hop distance of the beacon node i is obtained by the following equation to calculate:
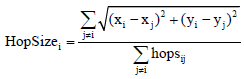 | (1) |
The average distance per hop is:
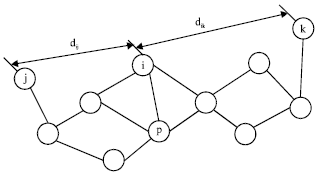 | |
| Fig. 1: | Schematic diagram of a DV-Hop localization algorithm example |
Assuming that p is to be positioned node, the number of hops is minimum between beacon nodes i and p, that distance is minimum from beacon nodes i to p. Thus, p obtains the average distance value at each hop from i, Cp = Ci, the estimated distance of each beacon node are Cphopspi, Cphopspj, from p. Then the position of the node p is calculated by using trilateration.
Improved DV-Hop localization algorithm: DV-Hop localization algorithm is the exchange of information based on network connectivity and distance vector, the straight-line distance is instead of hop distance and average hop distance is only obtained in the isotropic dense network, thus it is closer to the actual distance value, otherwise there is an error larger (Liu et al., 2009). In the practical application, WSN nodes are generally randomly distributed between the nodes and the beacon nodes, they are often not known linear path and the nodes are deployed in the monitor area, these nodes are not completely in the same plane and then the calculated resulting distance is the estimated value from unknown nodes along the ground curve to the beacon nodes. This is generally greater than the projection of the distance between unknown node and the beacon nodes in the horizontal plane (Xu and Liu, 2008). If you use this estimate to calculate the coordinates of the unknown node, it will exacerbate the error of the estimate coordinate values.
This section is for DV-Hop algorithm limitations in the randomly distributed network environment. First, the original algorithm to calculate the average distance per hop is improved by using minimum mean square error method and then the estimated distance between the unknown node and the beacon nodes is corrected by using the compensation factor, the positioning accuracy of the algorithm is improved.
Minimum mean square error method to calculate the average hop distance: The conventional methods are to calculate the average each hop distance value Ci by unbiased estimation and because the Eq. 2 value is equal to zero, the estimated value of the average hop distance is obtained (Ji and Liu, 2008).
| (2) |
where, m is the number of beacon nodes in network. The average hop distance value C is estimated by this method, the mean of their estimation error is zero but in general, the error meets the normal distribution, according to the parameter estimation theory, it is as the cost function of estimation error, using the mean square error is more rational than just to use variance or deviation (Zhang, 2002).
Therefore, we use the minimum mean square error method to calculate the average hop distance, if the Eq. 3 is minimized the estimated value of the average hop distance can be obtained.
| (3) |
If:
The average distance per-hop can be obtained based on minimum mean square error method and the estimated value is as follow:
 | (4) |
For example in Fig. 1, the average hop distance is obtained by calculating beacon nodes according to Eq. 4, it is:
Calculation of compensation coefficient: After the inter-node information are mutually forwarded in the first stage, each beacon node can get the coordinate information of other beacon nodes and minimum hops away. At this time, the actual distance of each beacon node calculated to the other beacon nodes based on the distance formula between two points, respectively and the average hop distance is calculated according to Eq. 4 . For example, the coordinates of the beacon node i and beacon node j are, respectively (xi, yi), (xj, yj). According to the distance formula, the obtained actual distance between them is dij, then the estimated distance is dijEST, which is calculated based on the average hop distance and minimum hops between them, the difference value between the estimated distance and actual distance is Δdij = |dijEST-dij|, thus this growth ratio of two beacon nodes is:
Finally, the information with the average distance per hop and growth ratio will be broadcasted in each beacon node, so that each unknown node receives the average distance per hop and the growth ratio of every pair beacon nodes and their values are stored. Thus each unknown node will obtain the following data: (1) Coordinate values of each beacon node, (2) To estimate the distance between the node own and each beacon nodes; between and (3) Ratio of increasing distance between each pair of beacon nodes.
Let the estimated distance be dijEST between the pair of beacon nodes i, j, the increasing ratio is mij, the estimated distance between unknown node p and beacon nodes i, j is, respectively dpiEST, dpjEST, then:
| (5) |
where, Dpij represents the deviation degree factor of connections in which the unknown node p deviate beacon nodes i, j, the greater Dpij, the greater the connection which the unknown node p deviates from the beacon nodes i, j. Since a single mij growth ratio does not fully reflect the communicated state between the node p and the beacon nodes i, j, in order to maximize the distance between unknown nodes and beacon nodes closer to the actual distance, the weighted average method is used (Huang and You, 2012), the compensation coefficient values of unknown node hops are calculated and there are least ones of three beacon nodes. Specific methods are as follows:
| • | Assuming the known hops from the unknown node p to all beacon nodes, three beacon nodes are identified at least hops. That is three beacon nodes nearest from an unknown node, they are beacon nodes i, j, k |
| • | First, the degree of deviation factor is calculated from the unknown node p to the connections between beacon node i and all the other beacon nodes, i.e.: |
| (6) |
where, n is the number of nodes in the beacon.
To take the smallest three ones of the degree of deviation factors from unknown node p to the connection lines between beacon nodes i and all other beacon nodes, they are Dpi1, Dpi2, Dpi3. According to the weighted average method, the corresponding compensation coefficient Mpi are calculated from the unknown node p to beacon node i.
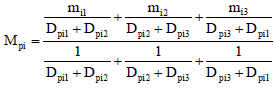 | (7) |
where, mi1, mi2, mi3 is, respectively the smallest three ones of the degree of deviation factors from unknown node p to the connection lines between beacon nodes i and all other beacon nodes. Similarly available from unknown node p to beacon node j, k, their corresponding compensation coefficient are Mpj, Mpk.
Distance between unknown node to beacon node corrected by using the compensation factor: By the above method, we obtained the appropriate compensation factor of nearest three beacon nodes from the unknown node, the estimation distance between them can be corrected. For example, the estimated distance between the unknown node p and the beacon node i is dpiEST the appropriate compensation coefficient is Mpi, the corrected distance is:
Similarly available, the corrected distances are:
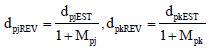 |
from p to beacon node j, k. Such corrected distance information of unknown node p is gotten after it got away from its recent three beacon nodes.
Calculation of coordinates of the unknown node: After the distance information between unknown node and its nearest three beacon node is obtained by the above method, the coordinates of the unknown node are calculated by using trilateration. However, the aforementioned calculated distance from unknown nodes to the nearest three beacon nodes have some errors with the actual situation, which may cause that the trilateration equations has no solution. To avoid this situation, we use the least squares method (Lin et al., 2009) to calculate the final coordinates of unknown nodes (Li et al., 2009; Bulusu et al., 2000; Chen et al., 2008; Langendoen and Reijers, 2003).
RESULTS AND DISCUSSION
By using Matlab, simulation comparative analysis is done on the DV-Hop localization algorithm and its improved algorithms based compensation coefficient. Let node distribution be 100x100 m square region, the sensor nodes are randomly distributed in the simulation area, the number of nodes is maintained at 150, each node has the same communication distance R = 35 m which the coordinate position of the beacon node is known, the unknown node coordinate position is obtained by algorithm. The different number of beacon nodes are set in simulation, the average location error is compared in the different algorithms. In wireless sensor network positioning, the general positioning error is defined as the ratio of error value between the node estimated position and the actual position node and communication radius, that is as follow:
| (8) |
wherein, ![]() and (x, y) are the estimated position and the actual position of the unknown node, the average location error is defined as:
and (x, y) are the estimated position and the actual position of the unknown node, the average location error is defined as:
is the positioning error of the unknown node i, un is the number of unknown nodes.
In this study, DV-Hop algorithm has been improved in two aspects: First, the network average, estimated value of each hop distance is calculated by using the minimum mean square error method, the second, compensation coefficient is introduced to correct the estimated distance between the unknown nodes and beacon nodes. The simulation is done in the improvement method of the first aspect, on this basis, further improvements are made in the simulation method of the second aspect, the positioning accuracy is compared between the improved algorithm and the original algorithm, the simulation results are shown in Fig. 2 and 3.
As can be seen from Fig. 2, when the number of participating position beacon nodes is increasing, the positioning error of the two algorithms are reduced. In the beginning, the positioning accuracy of the improved algorithm is little difference with the original algorithm but with the increase in the beacon nodes, by using minimum mean square error method, the calculated average network hop distance is closer to the actual average distance per-hop in random network, thereby the positioning error of nodes is effectively reduced, wherein the lower maximum value is reached to 8%.
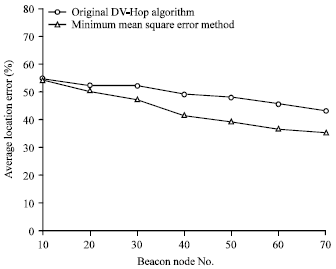 | |
| Fig. 2: | Calculation of average positioning error of two algorithms in the average hop distance by different methods |
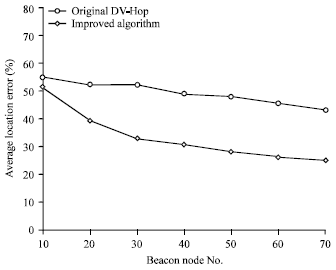 | |
| Fig. 3: | SNR comparison of three algorithms |
In Fig. 3, the estimated distance between the unknown nodes and the beacon nodes is corrected further by compensation coefficients and it is closer to the actual distance, thus the positioning error of unknown nodes is further reduced, it can be seen from the Fig. 3 that the positioning error is reduced by an average of 15-18% in the improved algorithm than traditional DV-Hop localization algorithm, positioning accuracy is significantly improved. When the number of beacon nodes is 60, in two algorithms, the improved amplitude of the positioning accuracy becomes smaller, the average location error changes are stabilized.
In summary, the average error is always less in this study improved positioning algorithm than the original DV-Hop algorithm (Niculescu and Nath, 2001, 2003) and there is good stability. However, during the execution of the algorithm, the growth ratio in the many beacon nodes is broadcasted and the compensation coefficients are calculated, the improved algorithm of this study will increase in terms of communication overhead and computation than the original algorithm.
CONCLUSION
In this study, because there are the limitations of DV-Hop algorithm in the random distributed network environment, first by using minimum mean square error method, the improvements are made to the original algorithm to calculate the average distance per hop and then the compensation factor is introduced to correct the distance between the unknown nodes and beacon nodes, DV-Hop algorithm is proposed based on a compensation coefficient. Through simulation, the improved algorithm average location error is less than one of the original algorithm and there is good stability. However, the positioning accuracy is improved in the improved algorithm which are adding the amount of communication and the amount of computation and the algorithm will increase the cost. How to maintain good location accuracy while reducing the overhead of communication and the amount of computation is the future content of further study.
REFERENCES
- Peng, Y. and D. Wang, 2011. A review: Wireless sensor networks localization. J. Electron. Meas. Instrum., 25: 389-399.
Direct Link - Niculescu, D. and B. Nath, 2001. Ad hoc Positioning System (APS). Proceedings of the IEEE Global Telecommunications Conference, Volume 5, November 25-29, 2001, San Antonio, TX., USA., pp: 2926-2931.
CrossRef - Niculescu, D. and B. Nath, 2003. DV based positioning in ad hoc networks. Telecommun. Syst., 22: 267-280.
Direct Link - Ji, W.W. and Z. Liu, 2008. Study on the application of DV-Hop localization algorithms to random sensor networks. J. Electron. Inform. Technol., 30: 970-974.
Direct Link - Liu, S., Q. Zhao and H. Wang, 2009. DV-Hop localization algorithm based on estimate of average hop distance and correction in position. Chin. J. Sens. Actuators, 22: 1154-1158.
Direct Link - Xu, J.B. and H.Y. Liu, 2008. Sensor localization algorithm in wireless sensor network based on different plane. Comput. Eng. Applic., 44: 115-117.
Direct Link - Huang, D.K. and T.T. You, 2012. Improved DV-Hop algorithm based on hop estimation. Comput. Moderniz., 12: 4-7.
Direct Link - Lin, J.Z., X.B. Chen and H.B. Liu, 2009. Iterative algorithm for locating nodes in WSN based on modifying average hopping distances. J. Commun., 30: 107-113.
Direct Link - Li, J., J. Zhang and L. Xiande, 2009. A weighted DV-Hop localization scheme for wireless sensor networks. Proceedings of the International Conference on Scalable Computing and Communications and 8th International Conference on Embedded Computing, September 25-27, 2009, Dalian, China, pp: 269-272.
CrossRef - Bulusu, N., J. Heidemann and D. Estrin, 2000. Gps-less low-cost outdoor localization for very small devices. IEEE Personal Commun., 7: 28-34.
CrossRef - Chen, H., K. Sezaki, P. Deng and H.C. So, 2008. An improved DV-Hop localization algorithm with reduced node location error for wireless sensor networks. IEICE Trans. Fundam. Electron. Commun. Comput. Sci., E91: 2232-2236.
CrossRef - Langendoen, K. and N. Reijers, 2003. Distributed localization in wireless sensor networks: A quantitative comparison. Comput. Networks, 43: 499-518.
CrossRef








