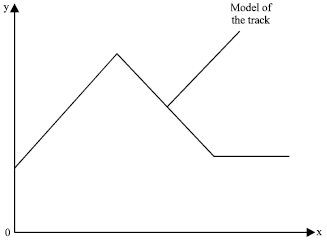
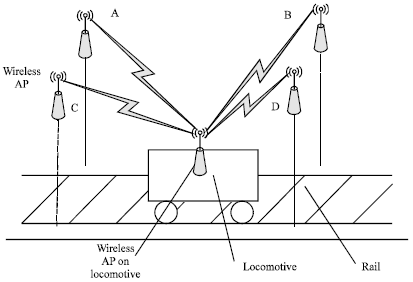
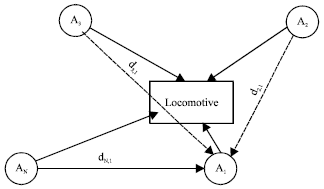
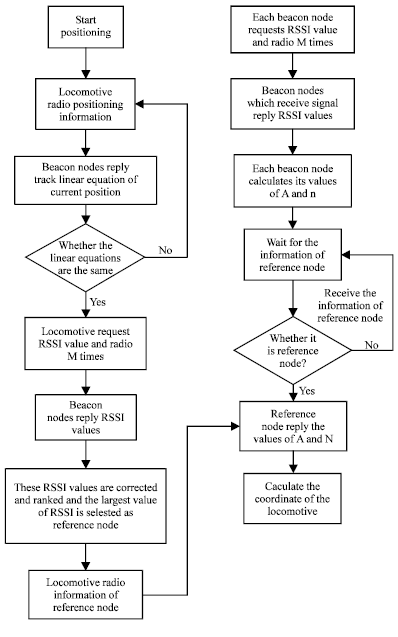
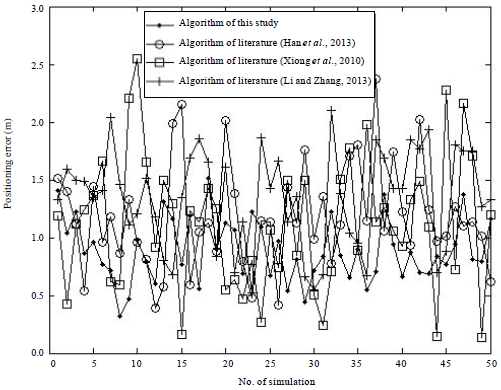
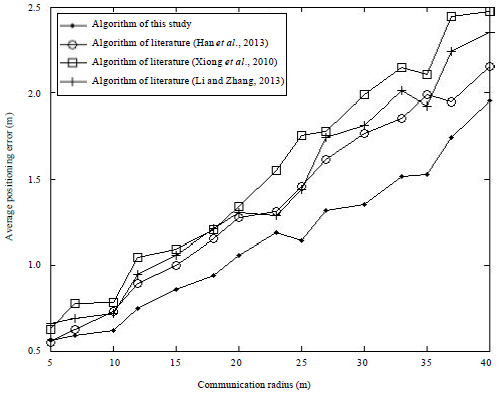
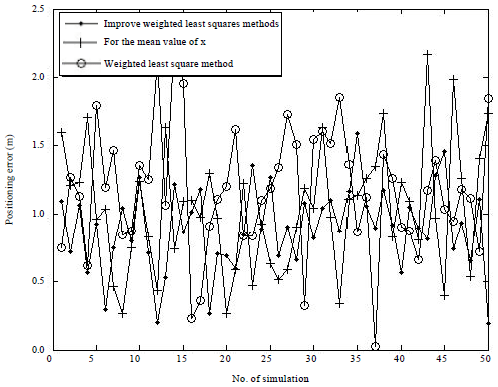
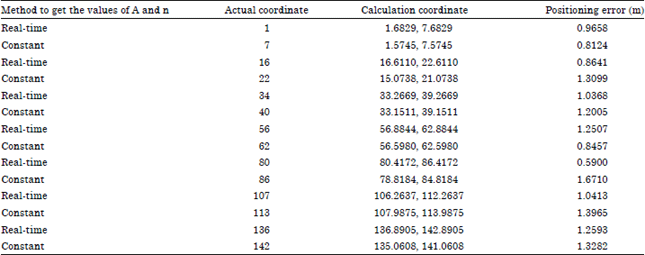
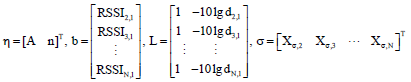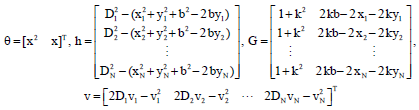Research Article
Research of Underground Mine Locomotive Positioning Algorithm Based on RSSI
School of Computer Science and Engineering, Anhui University of Science and Technology, Huainan, Anhui, 232001, China
Wang Kai
School of Computer Science and Engineering, Anhui University of Science and Technology, Huainan, Anhui, 232001, China
Han Jianghong
School of Computer and Information, Hefei University of Technology, Hefei, 230009, China