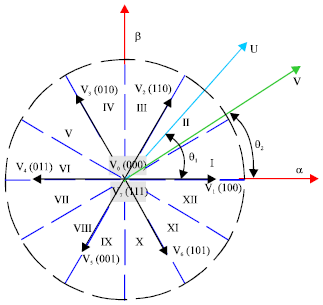
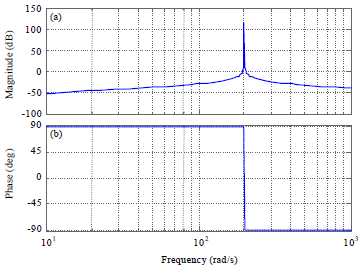
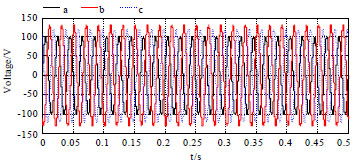
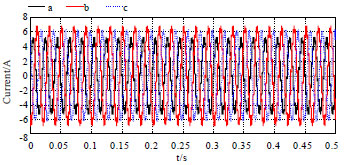
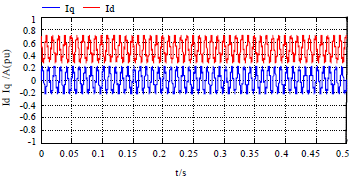
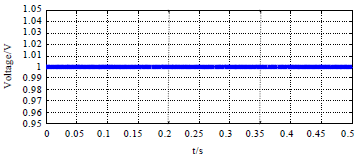
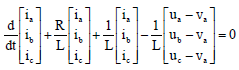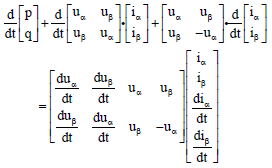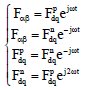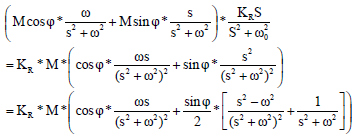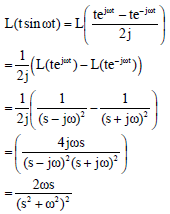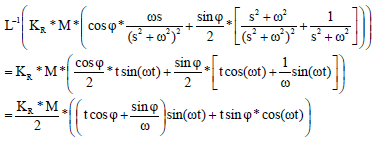Research Article
The Analysis and Implementation of Proportional Resonant Control Algorithm-based Pwm Inverter Imbalanced Grid-connected
School of Automatic Control, Northwestern Polytechnical University, Xi�an, 710072, China
Li Yu- Ren
School of Automatic Control, Northwestern Polytechnical University, Xi�an, 710072, China
Wang Peng
School of Automatic Control, Northwestern Polytechnical University, Xi�an, 710072, China
Liang Bo
School of Automatic Control, Northwestern Polytechnical University, Xi�an, 710072, China
FU Long- Fei
School of Automatic Control, Northwestern Polytechnical University, Xi�an, 710072, China