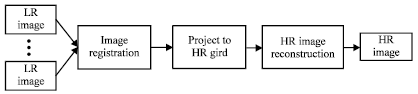
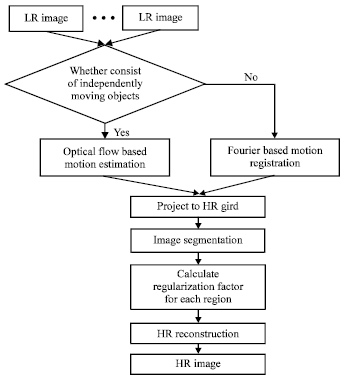
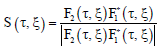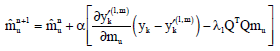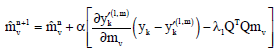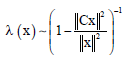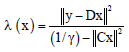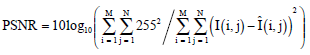Research Article
Region Adaptive Super Resolution Based on Total Variational Regularization
School of Electronics and Information, Northwestern Polytechnical University, Shaanxi, 710129, China
Hui Li
School of Electronics and Information, Northwestern Polytechnical University, Shaanxi, 710129, China
Mingui Sun
Swanson School of Engineering, University of Pittsburgh, PA 15213, United State of America