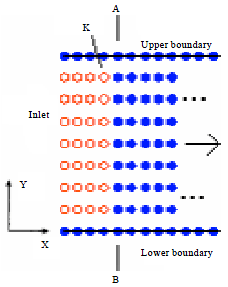
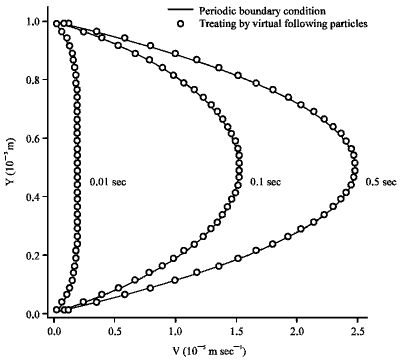
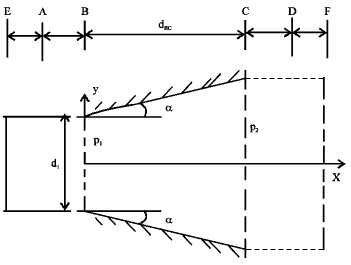
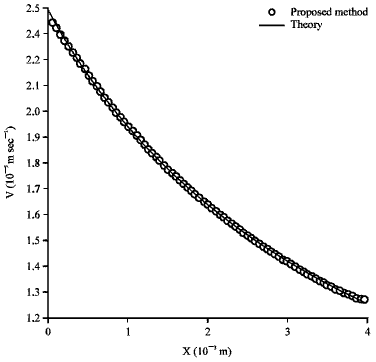
Research Article
A New Treatment for Boundary of Laminar Flow Inlet or Outlet in SPH
Department of Computer Science, Wuzhou University, Wuzhou, 543002, China
Jihong Huang
Department of Computer Science, Wuzhou University, Wuzhou, 543002, China
Wei Shi
Department of Mathematics and Physics, Wuzhou University, Wuzhou, 543002, China