ABSTRACT
The basic theories of Particle Swarm Optimization (PSO) is introduced and illustrated with flowchart. In this study one of its improved algorithms Adaptive Particle Swarm Optimization (APSO) is introduced. Characteristics of basic PSO algorithms are outlined. Some methods of APSO at present were introduced and analyzed with their parameters. Limitation of these APSO algorithms was analyzed. Pointed out that APSO algorithms can be improved with adjustment of parameters and some other hybrid APSO are referred. Finally, pointed out application of PSO needs to be extended, hybrid with other algorithms is thought a good way to improve APSO algorithm and applying the improved algorithm to complex problems is the goal of our study.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jse.2012.41.48
URL: https://scialert.net/abstract/?doi=jse.2012.41.48
INTRODUCTION
Particle swarm optimization algorithm (Particle Swarm Optimization, PSO) is raised by Kennedy and Eberhart (1995) through the foraging behavior of birds. It is based on Darwin's "survival of the fittest, survival of the fittest", the particle swarm optimization algorithm find the optimal solution through collaboration between individuals. Study found that PSO algorithm can be used to solve complex optimization problems (Kennedy and Eberhart, 1995). Just a few years, PSO algorithm has received a great development and successfully applied to many function optimization and engineering technology though being a hybrid with other algorithm (Feng and Wei, 2012).
It could be found that, through the analysis of biological communities, swarm intelligence of other complex behavior like their cooperation and competition between individuals can often produce some effective solutions to problems (Mataric, 1995). To avoid defects of basic PSO, it should be improved through combining other ideas of algorithm. In recent years, there is a kind of improved algorithm named adaptive PSO (APSO), which have been widely used. This study mainly discussed the development and applications of APSO.
BASIC PARTICLE SWARM OPTIMIZATION ALGORITHM
Ideas of PSO algorithm is originated from artificial mode, evolutionary computation theory and the flock of birds and is used for solving the optimization problem. Solution of the problem, called "particle", correspond with bird position in search space. Every particle has its position parameters and speed parameters and a fitness parameters can be used to decide good position or bad position. Particles search with two reference position. They were individual extreme value (pbest) and global extreme value (gbest) in the global version of PSO and pbest and local extreme value (some particles are replaced by better pbest, gbest and lbest. Particles search with position iteration and constantly updating their speed, best position in the iteration was written as lbest). New (1) and (2) was found in search process. It is assumed that solution space is D dimensions. The position and velocity of a particle i are D-dimensional vectors, expressed as:
and other vectors are also D dimensions. Iterative equation is as follows:
| (1) |
| (2) |
The dth dimension speed parameter of particle i in the kth iteration is expressed with Vid (k) and acceleration factors with C1 and C2. If C1 and C2 are too little , particles could not get to the target area; otherwise, particles would miss the target area. There is often a value 2, such as expression C1 = C2 = 2; The rand1.2 is a random number between 0 and 1; The dth dimension location of particle i in kth iteration is expressed as Xid(k); The individual extreme value of the dth dimension of particle i is expressed as pbestid, while global extreme value expressed as gbestd. The max of every dimension of particle is expressed as vdmax and its value could be chosen between -vdmax and vdmax to avoid particle fly away optimal solution or fall into local extreme value(Eberhart and Shi, 2001). Global PSO converge faster but easy to fall into local extreme value. So it can be a good idea to search approximately with global PSO at first and then with local PSO.
The flowchart is shown in Fig. 1: firstly, initialization. Initialize a particle group and its position and velocity parameters. With pbest of each particle being current location, calculate the fitness to get a gbest, record it.
 | |
| Fig. 1: | Flow chert of basic PSO |
Secondly, evaluation of the individual particles. Calculate the fitness value of individual particles, if better than the current pbest value, set pbest to be the position of the particle and update the individual extremes. If the best individual extremum of all particles is better than the current global extremum, also set gbest to be the particle position, record the serial number of the particle and update the global extremum. Thirdly, updating the particles, update each particle's velocity and position with Eq. 1 and 2. Final condition is used for testing tasks. The end conditions are generally the appropriate number of iterations or the error requirement. Meet the conditions and end, otherwise go back to the second step.
PSO operations, are achieved mainly by a few simple control parameters. By history and the best individual all the information and the search direction are given and the historical optimal position of each generation is maintained.
If you remove Vid(k) in the iteration equation of the speed, can be thought as a cross-algebra, each iteration of Vid(k) become the process of adapting. Overall, PSO is simple and effective, easy to control and can converge to optimal faster than the GA through being improved in most cases. Some improved methods are: cluster decomposition method (Kennedy, 2000), selection (Angeline, 1998), the neighborhood operator (Suganthan, 1999), PSO using stretching technology (Parsopoulos et al., 2001), no hope/wish to re-approach (Clerc, 1999), Breeding (Lovbjerg et al., 2001), SNT (sequential niche technique) (Van den Bergh, 2002), co-PSO (Van den Bergh and Engelbrecht, 2001). They research PSO by improving convergence rate, increasing diversity, ensuring convergence of PSO, etc., made some more suitable non-standard models of the PSO algorithm to the every kind of problems.
The paper (Eberhart and Shi, 1998) “Evolving artificial neural networks [R]” in Proceedings of International Conference on Neural) changes (1) into:
| (3) |
The dth dimension speed parameter of particle i in the kth iteration is expressed with Vid(k) and acceleration factors with C1 and C2, iteration weight with ω.
ADAPTIVE PARTICLE SWARM OPTIMIZATION ALGORITHM
In the process of solving the problem, the set of algorithm parameters of PSO has a great impact on the performance of the algorithm. When the problem is solved in algorithm, the different stages of evolution often require different combinations of parameters to meet the different needs of the search. For example, in the initial stages of the algorithm, the PSO need a larger inertia weight so that the algorithm can have more global exploration capability, meanwhile, the acceleration coefficient c1 can be increased to make the particles refer to their own search experience and avoid the algorithm prematurely to fall into a local optimum.
With the advance of the evolution, PSO gradually changes from the initial state to the convergence state of transformation, in this process, we need to reduce appropriately inertia weight, so that the algorithm can be better refined in the current convergence region, while also need to appropriately reduce the acceleration coefficients c1 and increase the acceleration coefficient c2 to make the algorithm converge better.
Adaptive particle swarm optimization can be described for some equations as follows:
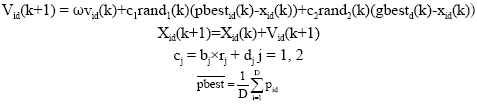 |
where, bj is a constant value 1.5, rj is a random value in the interval (0,1), dj is a constant value 1.5. bj and dj make the value of cj in the interval (0.5, 2). ω is linear value of iteration weight, for example, from 0.4 to 0.9. ![]() is average extremum of individuals, as a criteria for mutation.
is average extremum of individuals, as a criteria for mutation.
Flying time of each generation of particles is fixed at a standard particle swarm algorithm, resulting in the oscillation phenomenon and the inertia weight is linearly decreasing. It did not take full advantage of the additional information provided by the objective function, making the search direction not clear, slow convergence and easily trapped into local minima. The evolutionary process from the initial state to the convergence state is not a linear process, affected by various factors (such as algorithm parameters, operating strategy, the problem characteristics). Therefore, how to estimate the evolutionary state of the algorithm effectively and design effective control strategy of parameter according to different evolutionary state of the algorithm, which greatly affects acceleration of the search speed of the algorithm and the algorithm for accuracy. At the same time, how to avoid the algorithm to converge to a local optimum is also problem of particle swarm optimization to solve.
Based on the above analysis, in order to overcome falling into local optimum and premature convergence, the improved algorithms adaptive to change the parameters of PSO algorithm appear. Literature (Zhang et al., 2006) uses adaptive time-of-flight to improve the algorithm stability but the algorithm converge slowly. Eq. 2 is written as:
| (4) |
and T is expressed as:
where, T0 is longest time of flight, β is scale factor, which is constant and k is current number of generation, Kmax is the biggest generation number.
Literature (Liu and Lu, 2010) tested a particle swarm optimization using dynamic variable inertia weight, converge quickly but stability is not high. Article used Eq. 2 and 3 and improved ω as:
where, gmax is biggest number of iterations, g is current number of iterations, ωmax is maximum of iteration weight, ωmin is minimum of iteration weight.
Liu and Lu (2010) adaptively adjusted flight time and the inertia weight, improved stability and speed of convergence. In this articles the parameters changed is as follows:
ωk = exp(-gbestk/gbestk-1) |
The iteration number of kth particle is written as ωk, the global best value of kth and (k-1)th generation particle is expressed as gbestk, gbestk-1:
Xid(k+1) = Xid(k)+Vid(k+1)x0[1-βxk/Kmax] |
where, T0 is longest time of flight, β is scale factor, which is constant and k is current number of generation, Kmax is the biggest generation number.
Zhan et al. (2009) used mathematical statistics to analyze the distribution of the population and fitness information and define variable f called "evolutionary factor", which is Fuzzy partitioned with fuzzy logic to estimate the different evolutionary state of the algorithm and depending on the different evolutionary state, designed effective parameter of the algorithm to adaptively control strategy with Fuzzy logic in order to speed up the speed of solving optimization problems. Through testing, it could be found that it has better performance than basic PSO and other currently popular improved PSO algorithms such as fully informed PSO, dynamic multi-swarm PSO, comprehensive learning PSO etc. Its adaptation of the inertia weight is as follows:
The maximum increment or decrement between two generations is bounded by:
|ci (k+1)-ci (k)|≤δ i = 1, 2 |
where, δ is termed the “acceleration rate” in this study. Here, the interval [3.0, 4.0] is used to bound the sum of the two parameters. If the sum is larger than 4.0, then both c1 and c2 are normalized to:
ci = cix4.0/(c1+c2) i = 1, 2 |
The proposed algorithm by Jiang et al. (2012) can adjust inertia weight factor adaptively during different phases of the process according to the variation of the cosine function. In addition, the acceleration coefficients based on linear variation are disturbed under a certain condition. After comparing to other algorithms, the results show that this new algorithm can not only improve the convergence speed, but also ameliorate the premature convergence phenomenon obviously. Some parameters are as follows:
ω = (ωmax-ωmin) cos (π /Tmax)t/2+(ωmax+ωmin)/2 |
and
c1 = c1s+tx(c1e-c1s)/Tmax |
In addition to particle swarm optimization, there are other artificial intelligence algorithms that people are concerned about and research, such as genetic algorithm, Artificial Neural Network (ANN), Fuzzy Logic System (FLS), simulated annealing and ant colony algorithm. Combination with them in specific issues will be the main way to improve performance and application of the algorithms. There are currently some combined algorithms that merged ideas of algorithms (Shi and Eberhart, 2001). So, it could be try to use ideas in these algorithms to improve APSO.
The other improvement methods are, improvement based on the study of the c1 and c2, niche particle swarm algorithm and multi-swarm APSO with different inertia weight search or APSO with multi-strategy functioning in the search process.
APPLICATIONS OF APSO
PSO has been widely used for function optimization (Fukuyama, 2002), neural network training (Shi and Eberhart, 1998; Engelbrecht and Ismail, 1999; Van den Bergh and Engelbrecht, 2000; Zhang et al., 2000; Lu et al., 2003; Settles et al., 2003), fuzzy system (Wei and Zhou, 2010). Eberhart applied PSO in successfully analyzing the tremor diseases such as human Parkinson's disease (Eberhart and Hu, 1999). Tandon controlled the milling process with training neural networks by PSO (Tandon, 2001); Improved velocity updating equation is used to train fuzzy neural network in the study (Zhenya et al., 1998). Parsopoulos applied PSO for the solution of multi-objective optimization problem, maximizing and minimizing problem, integer programming problems and problems of locating all the global extreme. Researchers of Fuji company in Japan have applied improved PSO algorithm for the famous issue of Reactive Power and Voltage Control (Fukuyama and Yoshida, 2001).
People often encounter multi-objective optimization problems in practical engineering, for example, in the production process, people always want high output, less material, the saving hours of work; In digital filter design, people want larger attenuation of stop band and smaller mutations on the edge of band. APSO can be used for multi-objective optimization problem to solve these problems. Moreover, APSO also can be used in important industrial problems, such as PID controller design. There is an important significance to analyse multi-objective optimization problems deeply. Therefore, the APSO algorithm become important.
CONCLUSION
Since, 1998, the PSO has become an important branch of the PSO Algorithm. APSO is an important way of improving global search ability and convergence capabilities of the basic PSO algorithm. How to choose a better data structure and the optimization algorithm to improve the speed and efficiency is also a meaningful problem. Current research in this area is relatively scarce. Finally, how to apply the improved algorithm to complex problems is the goal of our study.
REFERENCES
- Mataric, M.J., 1995. Designing and understanding adaptive group behavior. J. Adaptive Behav., 4: 51-80.
CrossRef - Kennedy, J. and R. Eberhart, 1995. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Networks, 4: 1942-1948.
CrossRefDirect Link - Eberhart, R.C. and Y. Shi, 2001. Particle swarm optimization developments applications and resources. Proceedings of the Congress on Evolutionary Computation, May 27-30, Seoul, South Korea, pp: 81-86.
CrossRef - Kennedy, J., 2000. Stereotyping: Improving particle swarm performance with cluster analysis. Proceedings of the IEEE Congress on Evolutionary Computation, Volume 2, July 16-19, 2000, La Jolla, CA., USA., pp: 1507-1512.
CrossRef - Angeline, P.J., 1998. Using selection to improve particle swarm optimization. Proceedings of the International Conference Evolutionary Computation Intelligence, May 4-9, 1998, Anchorage, AK., USA., pp: 84-89.
CrossRef - Suganthan, P.N., 1999. Particle swarm optimiser with neighbourhood operator. Proceedings of the Congress on Evolutionary Computation, Volume 3, July 6-9, 1999, Washington, DC., USA., pp: 1958-1962.
CrossRef - Parsopoulos, K.E., V.P. Plagianakos, G.D. Magoulas and M.N. Vrahatis, 2001. Stretching technique for obtaining global minimizers through particle swarm optimization. Proceedings of the Workshop on Particle Swarm Optimization, April 6-7, 2001, Indianapolis (IN), USA, pp: 22-29.
Direct Link - Clerc, M., 1999. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. Proceedings of the Congress on Evolutionary Computation, July 6-9, 1999, Washington, DC., USA., pp: 1951-1957.
Direct Link - Van den Bergh, F. and A.P. Engelbrecht, 2000. Cooperative learning in neural networks using particle swarm optimizers. South Afr. Comput. J., 26: 84-90.
Direct Link - Zhang, C., H. Shao and Y. Li, 2000. Particle swarm optimisation for evolving artificial neural network. Proceedings of the IEEE International Conference on Systems, Man and Cybernencs, Volume 4, October 8-11, 2000, Nashville, TN., USA., pp: 2487-2490.
CrossRef - Lu, W.Z., H.Y. Fan and S.M. Lo, 2003. Application of evolutionary neural network method in predicting pollutant levels in downtown area of Hong Kong. Neurocomputing, 51: 387-400.
CrossRef - Zhenya, H., W. Chengjian, Y. Luxi, G. Xiqi, Y. Susu, R.C. Eberhart and Y. Shi, 1998. Extracting rules from fuzzy neural network by particle swarm optimisation. Proceedings of IEEE International Conference on Evolutionary Computation, May 4-9, 1998, Anchorage, AK., USA., pp: 74-77.
CrossRef - Eberhart, R.C. and X. Hu, 1999. Human tremor analysis using particle swarm optimization. Evol. Comput., 3: 1927-1930.
CrossRef - Fukuyama, Y. and H.A. Yoshida, 2001. A particle swarm optimization for reactive power and voltage control in electric power systems. Proceedings of the Congress on Evolutionary Computation, Volume 1, May 27-30, 2001, Seoul, Korea, pp: 87-93.
CrossRef - Shi, Y. and R. Eberhart, 2001. Fuzzy adaptive particle swarm optimization. Proceedings of the Congress on Evolutionary Computation, May 27-30, 2001, Seoul, South Korea, pp: 101-106.
CrossRef - Wei, W. and B. Zhou, 2010. Features detection based on a variational model in sensornets. Int. J. Digital Content Technol. Appl., 4: 115-127.
CrossRefDirect Link - Zhan, Z.H., J. Zhang, Y. Li and H.S.H. Chung, 2009. Adaptive particle swarm optimization. Syst. Man Cybern., 39: 1362-1381.
CrossRefDirect Link - Shi, Y. and R. Eberhart, 1998. A modified particle swarm optimizer. Proceedings of the World Congress on Computational Intelligence and IEEE International Conference on Evolutionary Computation, May 4-9, 1998, Anchorage, AK., pp: 69-73.
CrossRefDirect Link








