Research Article
Automatic Software Test Case Generation
Department of Computer Engineering, Alzahra University of Tehran, Vanak St., Tehran, Iran
H. Homayouni
Department of Computer Engineering, Alzahra University of Tehran, Vanak St., Tehran, Iran
Hasein Shirazee
Department of Computer Engineering, Islamic Azad University, Qazvin Branch, Qazvin, Iran









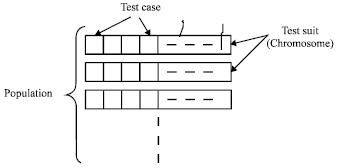
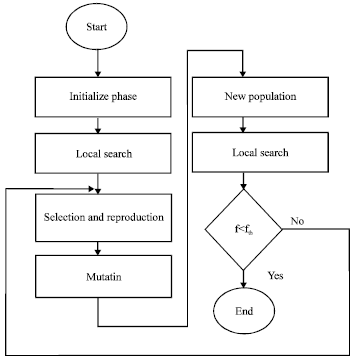



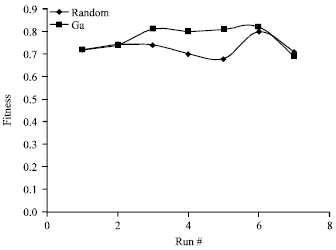
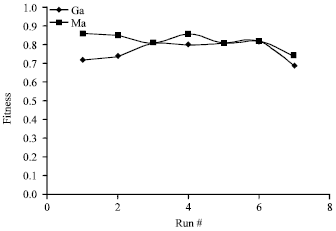
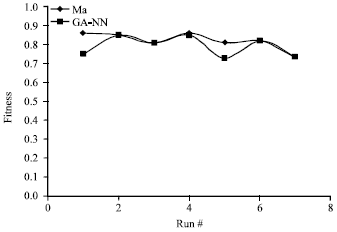
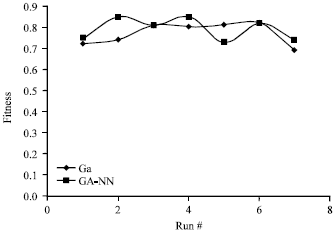
sandhia Reply
sir can u pls tell me the coding technique to generate the testcase
Hajar
Dear Sandhia
what do you exactly want to know?
sandhia
sir i am doing project based on test case reduction using case base reasonining can u give some hint for doing the coding for that project
Hajar
if you want to know about the coding language, I should say that it was via C#, and for implementing Neural network, i used Matlab. But if you want to know some thing about the coding logic i prefer you to read this Msc Thesis of a friend, which helped me to start with my project alot:
http://dspace.thapar.edu:8080/dspace/bitstream/123456789/253/1/91976.pdf
sandhia
sir thank u for ur response sir i found it was very helpfull for my project
Hajar Reply
if you have any other questions, plz let me know.
bahar Reply
Hello dear Ms.Homayouni
I'm Bahar Kashani ,student of Dr.keyvanpour.I'm working on automatic test case genaration. May i have your email address, to ask you some question?
I will appreciate you.