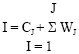Research Article
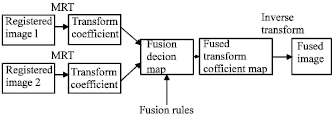
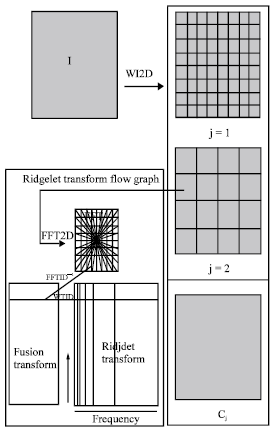
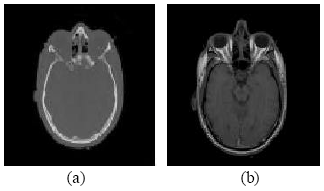
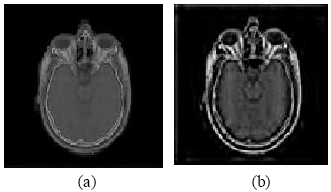
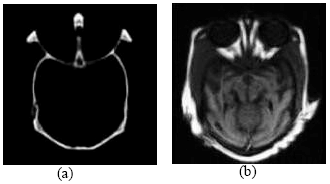
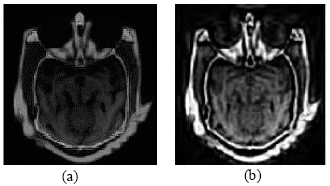
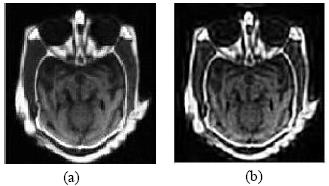
Medical Image Fusion Transforms-2D Approach
Department of Biomedical Engineermg, SSN College of Engineering, Chennai-600 025, India
S. Shenbaga Devi
Centre for Medical Electronics, Department of Electronics Communication Engl_neermg, College of Engineering, Guindy, Anna University, Chennai-600 (325, India