Research Article
Modelling and Analysis of Marine Reserve Creation
Faculty of Environment and Information Science, Kanagawa, Japan
H. Matsuda
Faculty of Environment and Information Science, Kanagawa, Japan
For the past decade there has been growing support among biologists for an expansion of the use of marine reserves, or areas protected from fisheries exploitation and other consumptive uses (Davis, 1989; Polacheck, 1990; Dugan and Davis, 1993; Roberts and Polunin, 1991; Man et al., 1995; Lauck et al.,1998; Sanchirico and Wilen, 1999). Most would agree that protected areas are likely to generate new consumptive and non-consumptive benefits, as well as research and education benefits and perhaps some existence values. Much of the empirical case study research on the ecological impacts of reserves supports this likelihoods, showing that essential fish habitat will gradually be restored, thereby increasing its growth potential relative to the nearby fishing grounds. A serious exploitation of reserve design issues should incorporate key ecological concepts dealing with the role of space in biological systems and the manner in which space affects fundamental processes of particular importance are notions of resource patchness and heterogeneity, biophysical linkages etc.
In most biological studies the main goal of the implementation of marine reserves is stock or ecosystem conservation. The political motivation behind the introduction of marine reserves has also mainly had this focus. Recently, however, economic studies of marine reserves have shifted focus towards taking into account the economics of fisheries as well (Holland and Brazee, 1996; Hannesson, 1998; Sanchirico and Wilen, 1999, 2001, 2002; Smith and Wilen, 2003). Hence the possibility of using marine reserves as a fisheries management tool has emerged. In the aftermath of failures first of input controls and then also to some degree of output controls in fisheries, the attention has now reverted back to a more complete form of input control, in the shape of closed areas. This research studies the modeling and analysis of marine reserve creation from both ecological and economic aspects.
Even though establishing a marine reserve in order to reap its benefits by harvesting in its neighborhood is a wishful thinking, it requires responsible planning to realize the fruits. While there are many example, both marine and terrestrial, to support that marine reserve have proven effective in bringing back the stocks (Bohnsack, 1998; Denny and Babcock, 2004; Russ et al., 2003; Russ and Alcala, 2004), there are also a few cases where failure to observe increased density of stocks of no-take regions is reported (Chapman and Kramer, 1999; Murawski et al., 2000). This may be attributed to the lack of adequate knowledge about the behavior and characteristics of the targeted species. Current economic models have ignored many recent ecological discoveries regarding population demography and have failed to explicitly model the presence of spatial heterogeneity in the resources recruitment rate. Within the marine ecological literature, it is well known that there are a magnitude of factors that influence the spatial and temporal distributions of the resource, yet economists have still failed to expand their models to incorporate it (Schnier, 2005). The model will incorporate spatial heterogeneity in the intrinsic growth rates. Arguments for natural spatial heterogeneity may correspond with those regions in which species congregate for spawning, possess advantageous from predators (Holbrook et al., 2000; Steele and Forrester, 2002; Holbrook and Schmitt, 2003).
In the present study, we consider a model representing the dynamics of a renewable resource in region under the assumption that this region is divided into two patches. One of these patches is considered to be a no-take reserve and the remaining adjacent patch is used for harvesting the resource. These assumptions seem very familiar in the economic literature dealing with economics related with marine or terrestrial reserves. The difference is that, in this study, the growth function is expanded to incorporate the presence of spatial heterogeneity in the resource recruitment. Sanchirico and Wilen (2001, 2002) also considered heterogeneity in the growth functions in their open-access and limited entry models, however, their growth parameters remain constant.
The Ecological Model and its Qualitative Properties
The pre-reserve growth of a population in a given area is assumed to follow the logistic path described by
| (1) |
with w as the population size at any time t, k is the carrying capacity and r is the intrinsic growth rate. Normalizing population by dividing population level with carrying capacity gives the growth equation:
| (2) |
where s = w / k,
Now, imagine that the population is divided into two sub-populations with the same homogeneous characteristics and that s = x + y, where x = w1 / k, y = w2/k and w = w1 + w2.
Growth Eq. 2 can now be written as
| (3) |
We also assume that Eq. 3 describes the post reserve growth of the total population in the absence of harvesting. Sub-area, 1 is the nature reserve (NR) and sub-area 2 is the harvest zone (HZ), with sub-populations x and y, respectively. The total population distribution area equals unity and sub-areas 1 and 2 equal m and 1-m, respectively, 0 < m <1. We assume that the two sub-areas, are delineated only on study and fishes are free to migrate between the two sub-areas depends on the differences. Assuming net migration is proportional to the difference in sub-population densities, net emigration from area 1, which equals immigration to area 2, is ![]() being the migration co-efficient. By assumption, harvest in HZ gives catch per unit effort (CPUE) proportional to the population density. The growth equation for each of the sub-populations x and y, adjusted for migration between sub-areas and harvesting, can now be written as
being the migration co-efficient. By assumption, harvest in HZ gives catch per unit effort (CPUE) proportional to the population density. The growth equation for each of the sub-populations x and y, adjusted for migration between sub-areas and harvesting, can now be written as
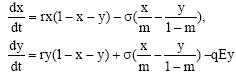 | (4) |
In most of the works with marine reserve the authors assume independent logistic growth for resident stock in each of the patches. But it turns out that such a coupled differential system does not represent dynamics of population in a patchy environment described above as it does not satisfy material balance in the ecosystem. Thus the model (4) has been suggested as an appropriate model to represent the dynamics of population in a patchy environment with homogeneous conditions.
Researchers studying the impacts of marine reserves have recognized the presence of spatial heterogeneity (Mangel, 2000; Schnier, 2005). These areas of comparative productive advantage can be referred to as biological “ hot spots” in the sense that populations that reside within these locations achieve higher recruitment rates than the surrounding areas due to the ecological advantages possessed within the region. Therefore, in the presence of biological hot spots, there will be two separate intrinsic growth rate parameters, rf and rR for the fishing grounds and the reserve. It is assumed that the fishery possesses a base intrinsic growth rate, rbase, for the majority of the fishery and a maximum rate, rmax, for the location possessing the highest level of recruitment. The spatial locations that lie between rbase and rmax represent the biological hot spots with the fishery and determine the degree of spatial heterogeneity present. For example, if there are I locations that possess a higher intrinsic growth rate than the base intrinsic growth rate the degree of heterogeneity in the fishery, denoted by mα, can be represented by mα = I/M, where, M is the total number of spatially distinct locations. To summarize, the intrinsic growth rates within the fishery grounds and reserve is a function of the base intrinsic growth rate, rbase, the maximum intrinsic growth rate, rmax, the percentage of the fishery that possesses biological hot spots, mα and the size of the reserve, m. For simplification, we assume that the fisheries managers will focus on reserving those areas within the fishery that possess a higher intrinsic growth rate and that the intrinsic growth rates lying within them. This assumption is consistent with what some ecologists have analyzed in their models of marine reserves (Lundberg and Jonzen, 1999; Mangel, 2000; Cote et al., 2001; Sala et al., 2002). Given this, the intrinsic growth rates within two juxtaposed regions is the average of all the locations and can be expressed as follows:
| (5) |
where G(r) represents the distribution of the intrinsic growth rates bounded by rmax and rbase. Incorporating these intrinsic growth rates, system (4) becomes
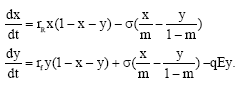 | (6) |
Let us now check if the model has an equilibrium point with positive sub-populations and whether this is a stable equilibrium. At equilibrium it follows from (6) that
| (7) |
and
| (8) |
where,![]()
Note that α and β are both positive, whereas A and B can be positive or negative.
The isoclines of the sub-populations are found from Eq. 7 and 8 and may be written as
| (9) |
| (10) |
The curve (9), which expresses the isoclines φ = 0, we shall denote C1 and the curve (10), which expresses the isoclines Ψ = 0, we shall denote C2. The shape of C1 and C2 is discussed below.
The equilibrium populations x* and y* can be found from Eq. 9 and 10.
Now we make the following graphical analysis, assuming x along the horizontal axis and y along the vertical axis. We have:
(a) C1 is a hyperbola with a vertical asymptote x = α, which enters the positive quadrant at (x, y) = (A, 0) if A > 0 and at the origin when A <0. This gives the three cases i = 1: A > α, i = 2: 0 < A < α and i = 3: A <0.
(b) Likewise, C2 is a hyperbola with a horizontal asymptote y = β, entering the positive quadrant at (x, y) = (0, B) when B > 0, or at the origin when B < 0. This gives the three cases j = 1: B >β, j = 2: 0 < B < β and j = 3: B < 0. This gives altogether nine cases that we represent as (i, j), where i, j = 1, 2, 3. For i = 1, β < y* < β, while i = 2, A < x* . Likewise, for j = 1, β < y* < β, while for j = 2, B < y* < β. In all eight cases with either i ≠ 3 or, j ≠ 3, there is a unique positive equilibrium; We show three examples in Fig. 4-6. This equilibrium is globally stable, attracting the entire positive quadrant; as indicated by in Fig. 4-6, schematically representing the direction field in the four separate regions that the positive quadrant is divided into by C1 and C2.
Threat of extinction may arise in (i, j) = (3, 3) case where there are two sub-cases, of which one is illustrated in Fig. 7. In this case origin is globally attracting the whole positive quadrant. The question about how to avoid extinction threatened by harvesting. Referring to Fig. 7 we consider the slopes of C1 and C2 at the origin. If
| (11) |
Then there is a positive equilibrium, for convenience, we denote the positive equilibrium by (x* , y* ), while the opposite inequality, there is no positive equilibrium.
From 9 and 10 and using the condition 11 we get, for the existence of the positive equilibrium as AB<αβ, (recall that in the case (3, 3) demonstrated in Fig. 7, we have A <0 and B<0). Which on simplification gives
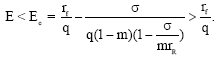 | (12) |
Effects of the Protective Patch on the Populations
It is well known that the population without protective patch is bound to be extinct if E ≥ rf/q.
Form Fig. 7, we see that if 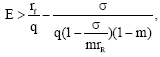 the protective patch can not eliminate the population’s extinction. We can conclude that if E increases in
the protective patch can not eliminate the population’s extinction. We can conclude that if E increases in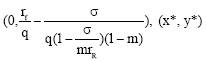 decreases monotonically and if the harvesting effort is large i.e.,
decreases monotonically and if the harvesting effort is large i.e.,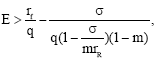 the population becomes extinct (Fig. 8). Population without protective patch becomes extinct inevitably as long as E≥rf/q. In this case, the protective patch is still workable, though it can not eliminate extinction in all situations, because the protective patch eliminates the possibility of extinction for
the population becomes extinct (Fig. 8). Population without protective patch becomes extinct inevitably as long as E≥rf/q. In this case, the protective patch is still workable, though it can not eliminate extinction in all situations, because the protective patch eliminates the possibility of extinction for
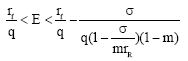 |
Putting these pieces together, we can draw a final conclusion that the protective region is practicable in the management of resources population, though in some cases the extinction can not be eliminated.
In practical management, the environmental conservation should be more important than the economic benefits, since it is unwise to eliminate any resource population. The ultimate purpose of establishing protective patch for the resources population is to produce more benefits.
Optimal Harvesting
Here we consider an optimal harvesting problem associated with the dynamical system (6). This study is aimed at not only solving the optimal harvest problem associated with the considered dynamic system but also to study the role of the no-take reserve, impact of heterogeneous growth in improving the bio-economics of the ecosystem. Thus we derive policies to maximize net benefit to the harvester for a given situation and also find conditions in terms of the parameters of the system which can improve the net revenue to the harvesting agency. This is done by assuming the measure of spill over support given by the no-take reserve to the harvesting region by tracking the shadow value of the stock in the no-take reserve.
Let p and c represent price per unit harvest and cost per unit effort respectively. Now, let us consider the following optimal harvesting problem:
| (13) |
subject to (6) and 0 ≤ E ≤ Emax, where Emax is the upper bound of the harvesting effort and δ is the instantaneous rate of annual discount.
If λ1 and λ2 (t) represent the current value of the shadow price of the resource in patch 1 and 2 respectively, then the current value Hamiltonian (Kamien and Schwartz, 1981) associated with the optimal harvesting problem is given by
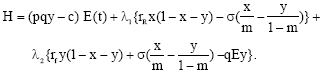 | (14) |
From the necessary conditions for optimality (Clark, 1990), the following condition is valid along the optimal solution
| (15) |
with the dynamics of the associated shadow prices described by
| (16) |
| (17) |
We observe that along an optimal equilibrium solution of the considered problem we have
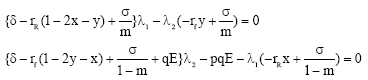 |
In view of Eq. 15, if the equilibrium solution (x* (E), y* (E)) satisfies
we have
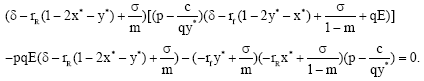 | (18) |
When an optimal stationary solution (x* , y* ) exists, the associated optimal fishing effort E* satisfies
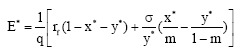 |
with the profit
Now our job is to reach the optimal solution optimally from the initial state (x(0), y(0)). Since the considered optimal control problem is linear in its control variable E, the optimal harvest policy will be a combination of bang-bang and singular controls (Pontryagin et al., 1962). Taking advantage of the linearity of the Hamiltonian in the control variable, we can define optimal approach paths as a consequence of bang-bang policy. Let us define
where S(t) = pqy-c-λ2qy. Let T be the time at which the path (x(t), y(t)) generated by bang-bang control reaches the state (x*, y*). Then the optimal control policy will be
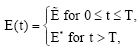 |
and the optimal path is given by the trajectory generated by the above optimal control. In view of the global stability property of the interior equilibrium of system (6) we can also reach the singular optimal solution through a suboptimal path by choosing the control policy E(t) to be equal to E* for all t. Thus we have two paths to approach the optimal singular solution. One is the most rapid approach path obtained by implementing the optimal harvest effort policy whch is called the optimal path and the other is by applying the optimal singular effort right from t = 0 which yields a sub optimal path. The advantage in choosing optimal path is that it reaches the optimal singular solution earlier than the suboptimal path.
Simulation Results
Here, we assign some values to the parameters of the system (6) and compute numerical solutions for optimal control problem. We assume the values of c = 0.4, q = 0.1, δ = 0.001, σ = 0.1, p = 7. The cases of homogeneous intrinsic growth rate and heterogeneous intrinsic growth rates are simulated separately.
Homogeneous Growth Rate
In this case it is assume that rf = rR = 1, m = 0.3 and mα = 0. For these values of the parameters we get the optimal singular effort 0.73, optimal singular stock (0.32, 0.63) and optimal singular revenue is 31.34.
Figure 1 and 2 clearly indicate that, creating no fishing zone increases the total biomass but reduce the present value of net revenues.
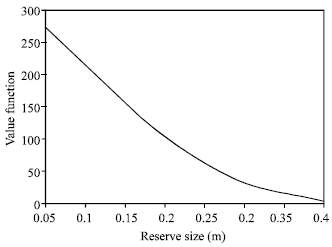 | |
| Fig. 1: | Relationship between value function and reserve size at equilibrium |
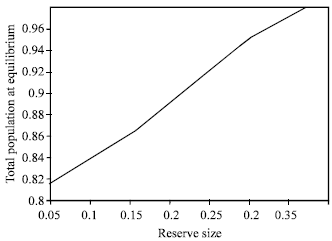 | |
| Fig. 2: | The relationship between total population and reserve size |
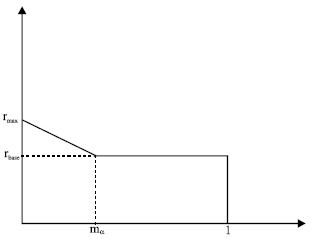 | |
| Fig. 3: | Heterogeneous intrinsic growth rates |
Heterogeneous Growth Rates
In order to study the effect of heterogeneous growth rates, it is necessary to assume a distribution for the intrinsic growth rate, G(r).
Figure 3, provides a graphical illustration of the assumed distribution of intrinsic growth rates used in the simulation. It is further assumed that the marine reserve will encompass those areas of higher intrinsic growth before the lower values.
There are two conditions must be considered to determine the intrinsic growth rates within the fishing grounds and the reserve. Condition one occurs when the reserve size m, is less than or equal to the degree of heterogeneity mα within the fishery and condition two occurs when the reserve size exceeds mα.
Condition 1. m ≤ mα.
In this case intrinsic growth rates for reserve and fishing ground becomes
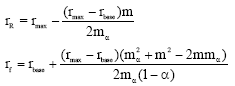 |
respectively.
Condition 2. m > mα.
In this case intrinsic growth rates for reserve and fishing grounds becomes
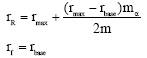 |
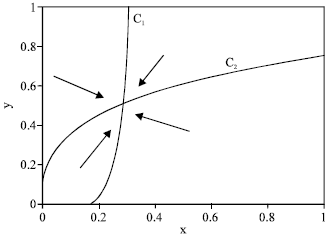 | |
| Fig. 4: | Equilibrium and direction field for case (1, 1). Parameter values are rmax = 0.8, rbase = 0.4, q = 0.1, σ = 0.15, m = 0.3, mα = 0.3, E = 1.5 |
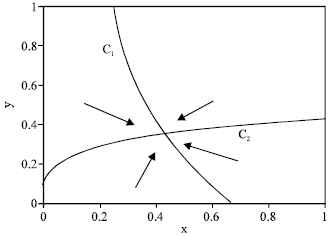 | |
| Fig. 5: | Equilibrium and direction field for case (2, 2). Parameter values are rmax = 1.4, rbase = 0.6, q = 0.1, σ = 0.1, m = 0.3, mα = 0.3, E = 4 |
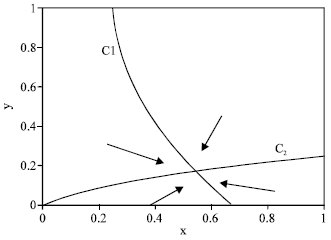 | |
| Fig. 6: | Equilibrium and direction field for case (2, 3). Parameter values are rmax = 1.4, rbase = 0.6, q = 0.1, σ = 0.1, m = 0.3, mα = 0.3, E = 11 |
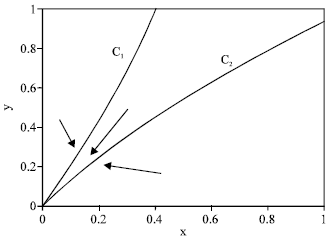 | |
| Fig. 7: | No positive equilibrium, a case of type (3, 3). Parameter values are rmax = 0.8, rbase = 0.4, q = 0.1, σ = 0.7, m = 0.3, mα = 0.3, E = 11 |
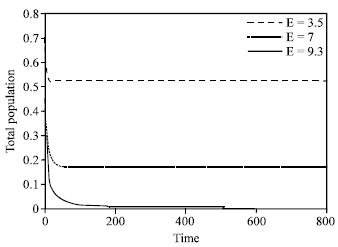 | |
| Fig. 8: | Relationship between total population and harvesting effort |
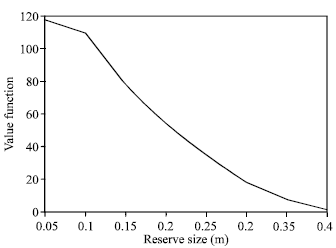 | |
| Fig. 9: | Relationship between value function and reserve size |
In this case the origin is globally attracting the whole positive quadrant, i.e., parameter values and harvest effort combined threatens to extinguish the population.
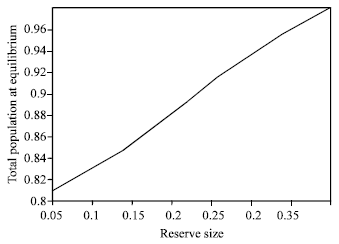 | |
| Fig. 10: | Relationship between total population and reserve size |
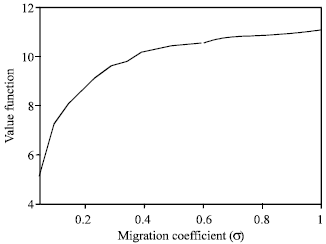 | |
| Fig. 11: | Relationship between value function and migration coefficient |
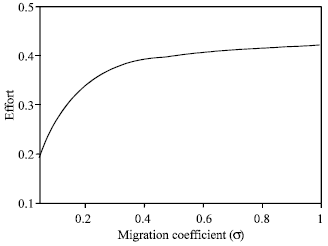 | |
| Fig. 12: | This figure represents the optimal singular effort to maximize net revenue for different migration co-efficient |
The Fig. 8 shows that the protective patch can not eliminate extinction in all situations.
Figure 9 and 10 indicate that areas of higher growth rate are also more viable as profitable fishing sites and therefore reserving them does not provide sufficient spillover to benefit the fishing grounds via migration.
Figure 11 and 12 indicate that both harvesting effort and value function increases with migration coefficient. Therefore, MPA is more effective for a resource with relatively high mobility.
In this work, impacts of MPA creation have been investigated, on both economic and biological perspectives. It is assumed that protected areas are those areas with higher intrinsic growth rates. The current analysis shows that MPAs is practicable in the management of resources population, which is beneficial to the conservation of ecological environment and resource population, though in some cases the extinction can not be eliminated. The establishment of MPAs could help maintain high fish biomass in the marine habitat. It is also proved that when the interior equilibrium point exists it is globally asymptotically stable. Optimal solution in the equilibrium case is also discussed. Biological and bioeconomic interpretations of the results associated with the optimal solutions are explained.
The simulations (both homogeneous and heterogeneous) indicate that no-fishing zone simply reduce the present value of net revenues. Hence the areas of higher growth rate does not provide sufficient spillover to benefit. This result was also found in Sanchirico and Wilen (1998) and was attributed to the fact that high productivity areas provide the highest pre-reserve returns to fishermen and hence the highest opportunity costs of closures. So some of the conventional wisdom that might be suggested from purely biological objectives (e.g., to close high productive patches) may be reversed when one considers economic costs to the industry of reserve sitting.
We notice that the effects of a variation of the migration coefficient is very significant. As migration coefficient increases both the harvesting effort and value function increases. This is a logical conclusion given that if the reserve population fails to migrate into the fishing grounds, the fishery will be divided into two distinct populations and the harvest will be truncated. This contradicts the result of Ami et al. (2005), where it is mentioned that the effect of the migration coefficient is not very significant.
In the case where the amount of the resource spillover is not sufficient, MPA may lead to loss for the fishery sector. If managers concerns are the only fishery sector benefits, MPA implementation must be given up. If the objective of fishery managers takes into account other potential benefits, social value of a MPA still positive.
Acknowledgement
Authors would like to thank Japan Society for the Promotion in Sciences for financial support of this research (P05109).