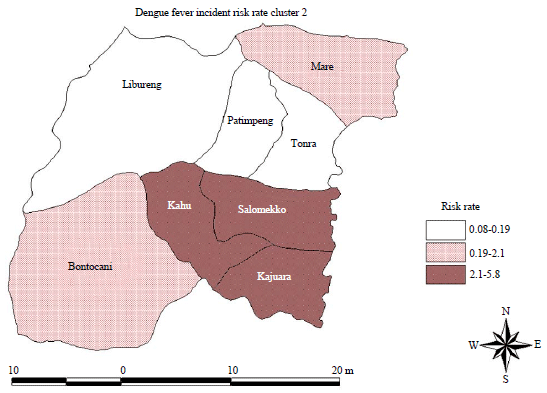
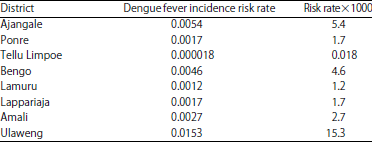
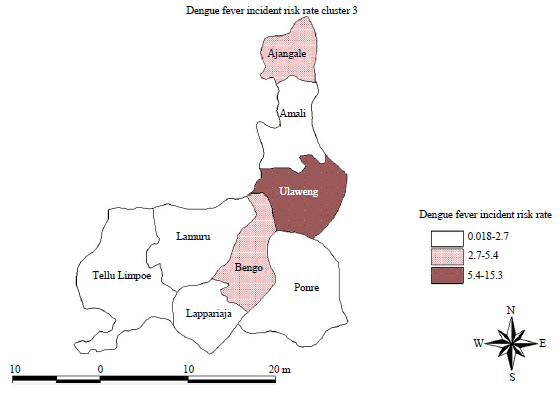
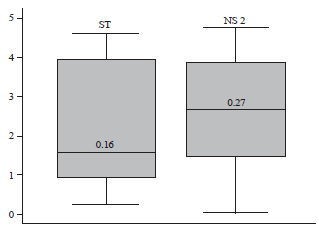
Research Article
Forecasting of Dengue Disease Incident Risks Using Non-stationary Spatial of Geostatistics Model in Bone Regency Indonesia
Department of Biostatistics, Faculty of Public Health, Hasanuddin University, Indonesia
Amran Rahim
Department of Mathematic, Faculty of Mathematic and Natural Sciences, Hasanuddin University, Indonesia
Anwar Mallongi
Department of Environmental Health, Faculty of Public Health, Hasanuddin University, Indonesia
LiveDNA: 62.16355