Research Article
Bilateral Risky Partial Differential Equation Model for European Style Option
Department of Mathematics, Ekiti State University, Ado Ekiti, Nigeria
LiveDNA: 234.23213
Florence Dami Ayegbusi
Department of Mathematics, First Technical University, Ibadan, Nigeria









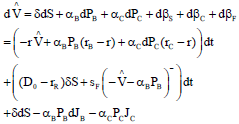
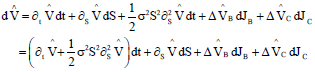
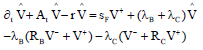
Dr. Fadugba Sunday E. Reply
This research article presents a bilateral risky partial differential equation model for the European style option. This is an eye opener in the field of financial mathematics.