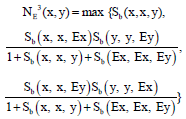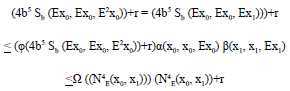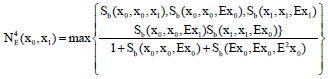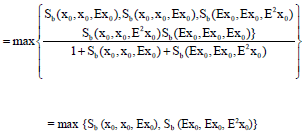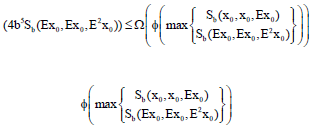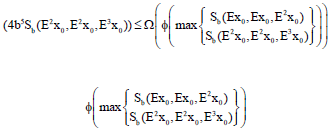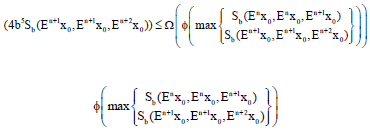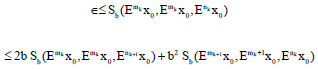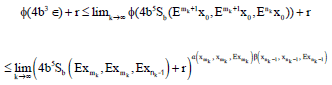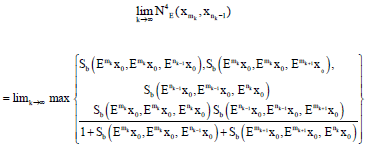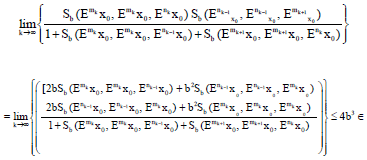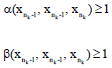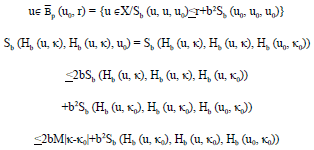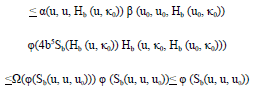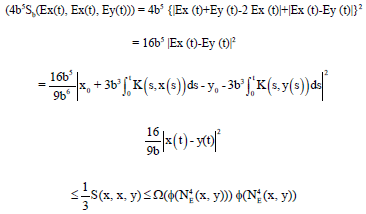Research Article
Fixed Point Theorems in Ordered Sb-Metric Spaces by Using (α, β)-Admissible Geraghty Contraction and Applications
Department of Mathematics, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, 522502 Andhra Pradesh, India
Gajula Naveen Venkata Kishore
Department of Mathematics, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, 522502 Andhra Pradesh, India
LiveDNA: 91.22413
Muhammad Sarwar
Department of Mathematics, University of Malakand, Chakadara Dir (L), Khyber Pakhtunkhwa, Pakistan
LiveDNA: 92.92
Nalamalapu Konda Reddy
Department of Mathematics, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, 522502 Andhra Pradesh, India