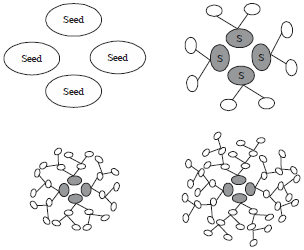
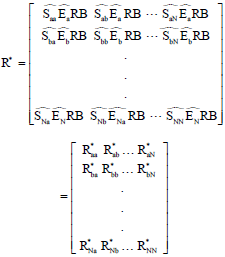
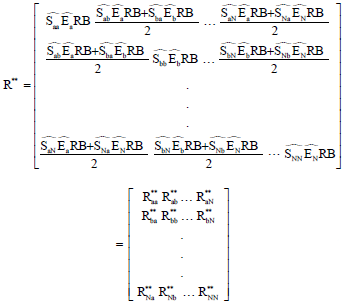
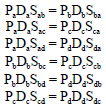Research Article
Population Proportion Estimator of Respondent Driven Sampling for Non-dichotomous Variables, Data Smoothing Approach
National Population Studies and Comprehensive Management Institute, Tehran, Iran
LiveDNA: 98.12751
Mahsa Saadati
National Population Studies and Comprehensive Management Institute, Tehran, Iran