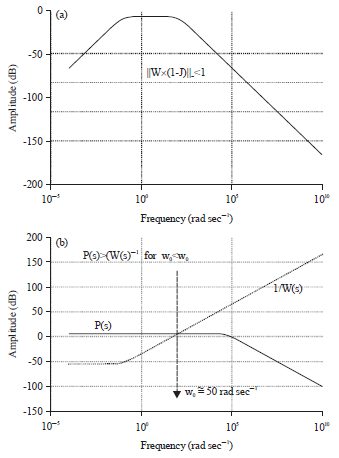
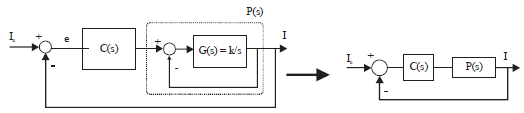
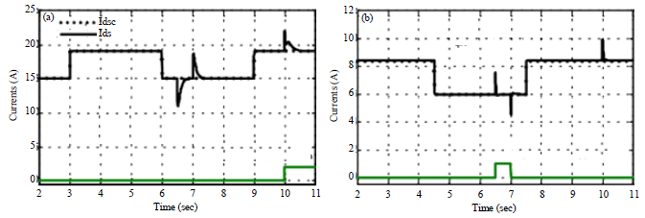
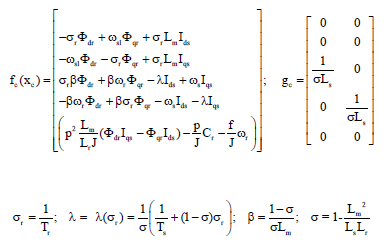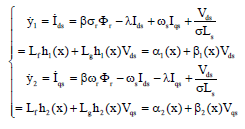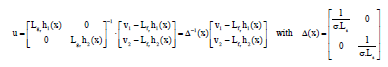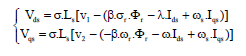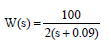Research Article
Nonlinear Control of an Induction Machine using Robust Controller based on H∞ Algorithm
Ecole Superieure Africaine des TIC (ESATIC), Abidjan, Cote d`Ivoire
Pamela Yoboue
Ecole Superieure Africaine des TIC (ESATIC), Abidjan, Cote d`Ivoire
Paul Kouakou
Universite Nangui Abrogoua, (UNA), Abidjan, Cote d`Ivoire
Pierre Tety
Institut National Polytechnique Felix Houphou�t Boigny (INP-HB), Yamoussoukro, Cote d`Ivoire
Raoul Zamble
Ecole Superieure Africaine des TIC (ESATIC), Abidjan, Cote d`Ivoire