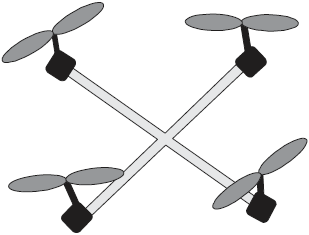
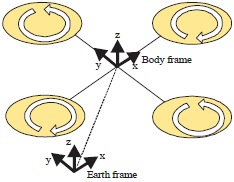
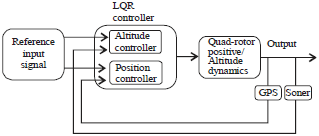
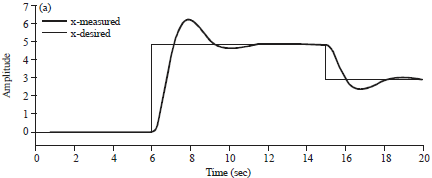
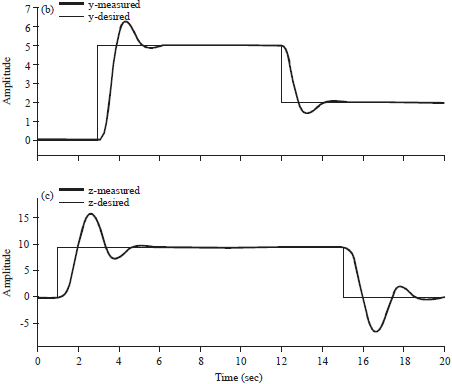
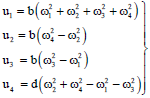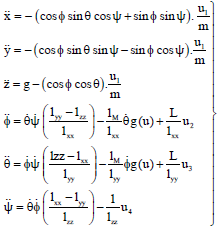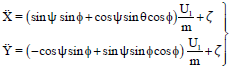Research Article
LQR Based Controller Design for Altitude and Longitudinal Movement of Quad-rotor
British Malaysian Institute (UniKL BMI), University Kuala Lumpur, Malaysia
Kushsairy Kadir
British Malaysian Institute (UniKL BMI), University Kuala Lumpur, Malaysia
M. Kamran Joyo
British Malaysian Institute (UniKL BMI), University Kuala Lumpur, Malaysia