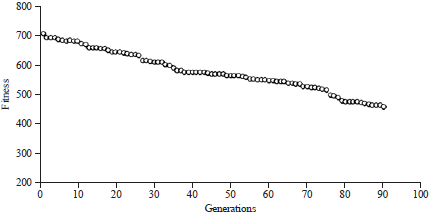
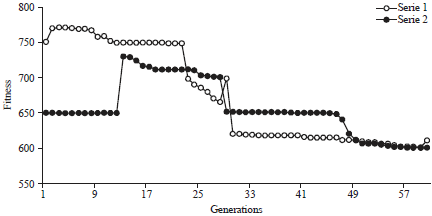
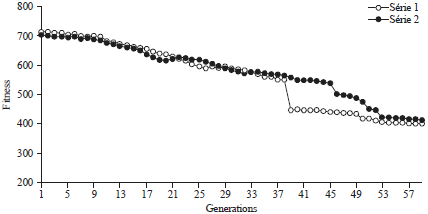
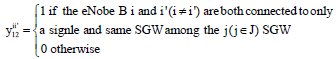Research Article
Assigning eNode B to Switches in LTE Advanced Network by an Approach Genetic
Ecole Superieure Africaine des TICs (ESATIC), Direction de la Recherche et l�Innovation Technologique (DRIT), Boulevard de Marseille, Abidjan-Treichville Zone 3-km 4, C�te d`Ivoire
Brou Pacome
Ecole Superieure Africaine des TICs (ESATIC), Direction de la Recherche et l`Innovation Technologique (DRIT), Boulevard de Marseille, Abidjan-Treichville Zone 3-km 4, C�te d`Ivoire
Diaby Moustapha
Ecole Superieure Africaine des TICs (ESATIC), Direction de la Recherche et l`Innovation Technologique (DRIT), Boulevard de Marseille, Abidjan-Treichville Zone 3-km 4, C�te d`Ivoire
Asseu Olivier
Ecole Superieure Africaine des TICs (ESATIC), Direction de la Recherche et l`Innovation Technologique (DRIT), Boulevard de Marseille, Abidjan-Treichville Zone 3-km 4, C�te d`Ivoire
Aka Boko Matthieu
Laboratoire des Mathematique Informatique (LMI), Universite Nangui Abrogoua (UNA), Abidjan (Axe Abobo-Adjame), C�te d`Ivoire
Konate Adama
Ecole Superieure Africaine des TICs (ESATIC), Direction de la Recherche et l`Innovation Technologique (DRIT), Boulevard de Marseille, Abidjan-Treichville Zone 3-km 4, Cote d`Ivoire
Oumtanaga Souleymane
Institut National Polytechnique-Houphouet Boigny (INP-HB), Laboratoire de Recherche en Informatique et Telecommunication (LARIT), Abidjan-Cocody Danga, Cote d`Ivoire