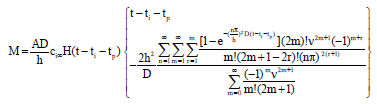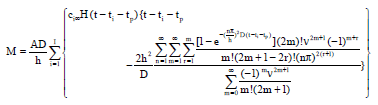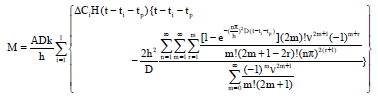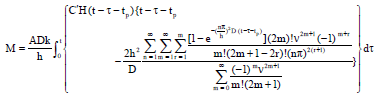Research Article
Diffusion of Chloride in Concrete under Fluctuating Environmental Conditions
Center for General Education, TransWorld University, 64043 Yunlin, Taiwan, Republic of China
Ching-Chang Lin
Department of Civil Engineering, Feng-Chia University, Taichung, Taiwan, Republic of China