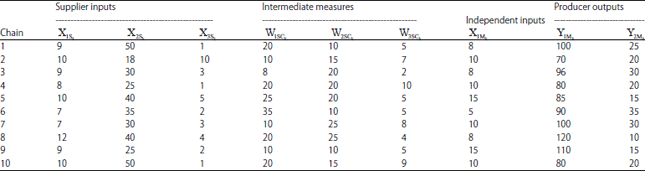
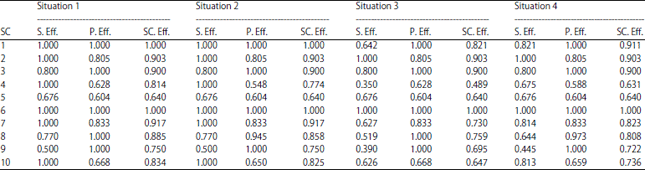
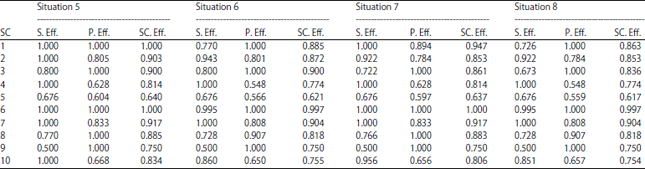
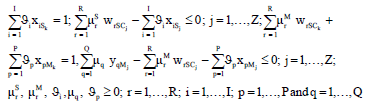Research Article
Measurement of Dyadic Supply Chains Efficiency under New Assumptions Using DEA Models
Faculty of Art and Sciences, Northern Border University, Rafha, Saudi Arabia
Abdelwaheb Rebai
Faculty of Economics and Management of Sfax, University of Sfax, Sfax, Tunisia