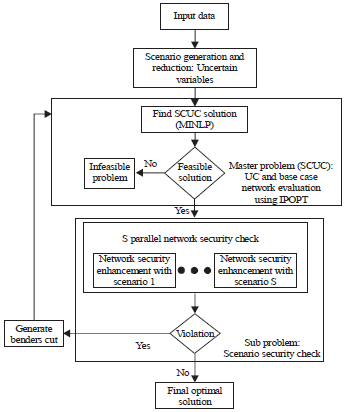
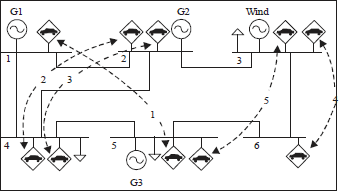
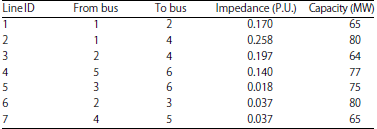
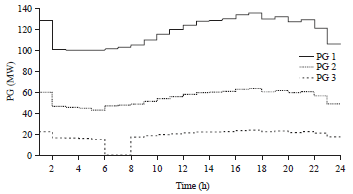
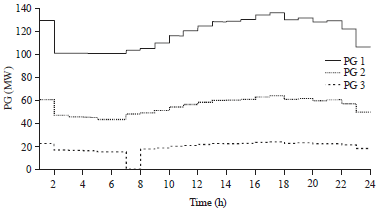
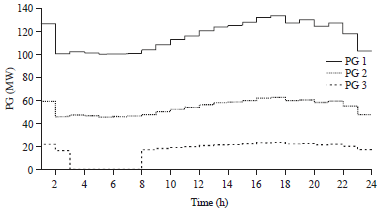
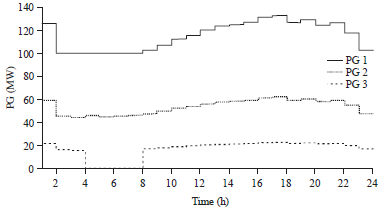
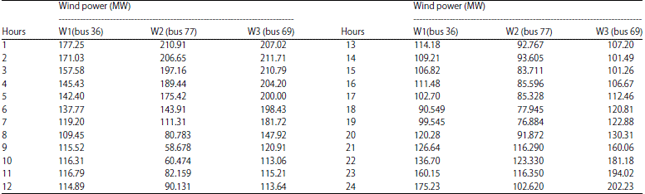
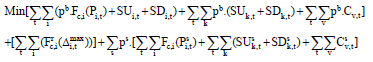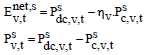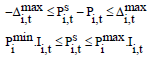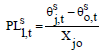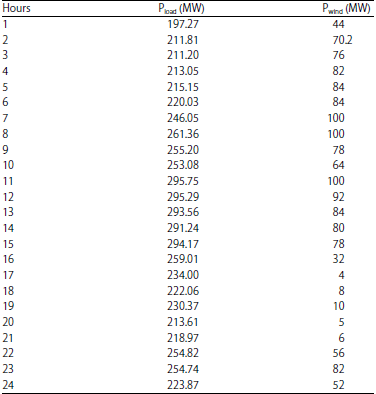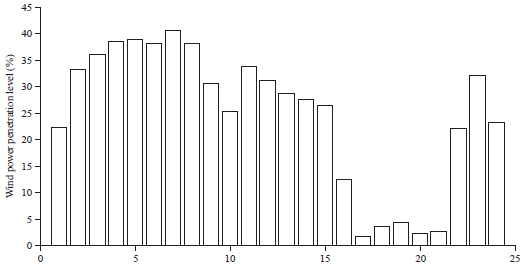Research Article
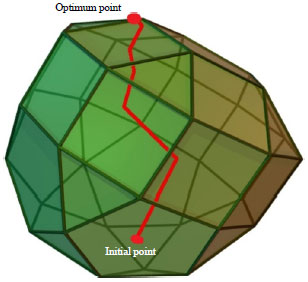
An Interior Point Optimization Method for Stochastic Security-constrained Unit Commitment in the Presence of Plug-in Electric Vehicles
Young Researchers and Elite Club, Dariun Branch, Islamic Azad University, Dariun, Fars, Iran
Masoud Jokar Kouhanjani
Young Researchers and Elite Club, Dariun Branch, Islamic Azad University, Dariun, Fars, Iran
Amir Pourjafar
Department of Power and Control, Engineering Faculty No. 1, Shiraz University, Shiraz, Iran
Seyedbehnam Beladi
Department of Power and Control, Engineering Faculty No. 1, Shiraz University, Shiraz, Iran