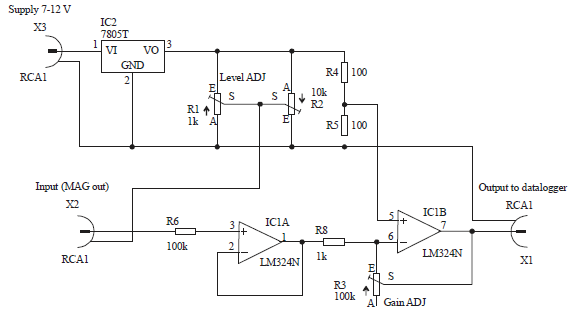
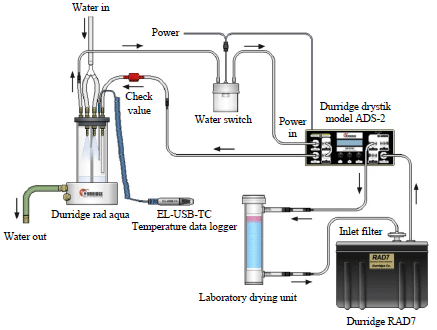
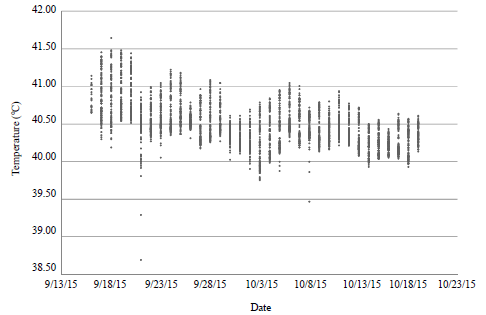
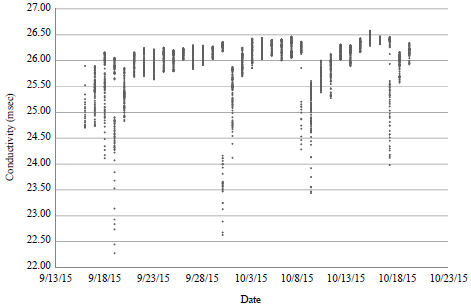
Research Article
Seismic Activity and Geochemical Monitoring of Thermal Waters in Thermopylae
Department of Electrical Engineering, ATEI of Central Greece, Lamia 35100, Greece
K.E. Anagnostou
Department of Electrical Engineering, ATEI of Central Greece, Lamia 35100, Greece
P. Avlakiotis
Department of Electrical Engineering, ATEI of Central Greece, Lamia 35100, Greece
S. Kotsopoulos
Department of Electrical Engineering, National Technical University of Patra, Patra, Greece
C. Liolios
Department of Electrical Engineering, ATEI of Central Greece, Lamia 35100, Greece
G.S. Perantzakis
Department of Electrical Engineering, ATEI of Central Greece, Lamia 35100, Greece
A. Lygdis
Department of Electrical Engineering, ATEI of Central Greece, Lamia 35100, Greece