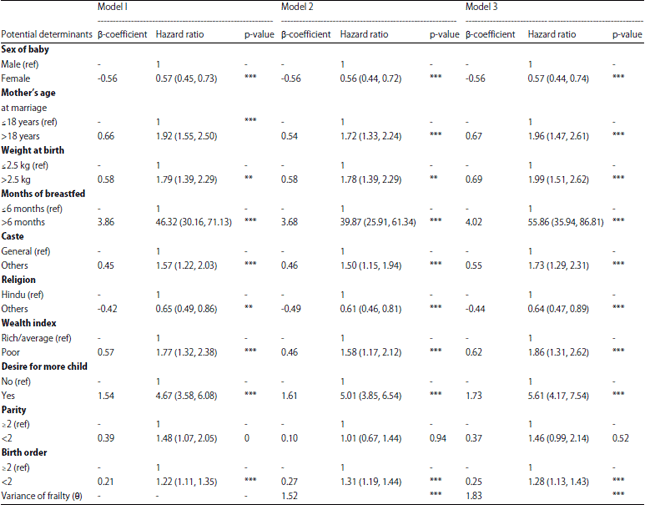
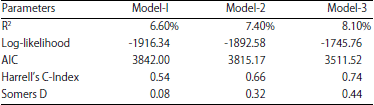
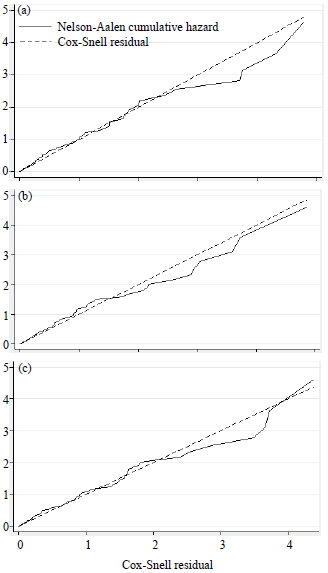
Research Article
A Study on Childhood Mortality Using Shared Frailty Modeling Approach
Department of Community Medicine, ESI-Post Graduate Institute of Medical Sciences and Research, Kolkata, India
Ram Janak Yadav
National Institute of Medical Statistics, Indian Council of Medical Research, New Delhi, India