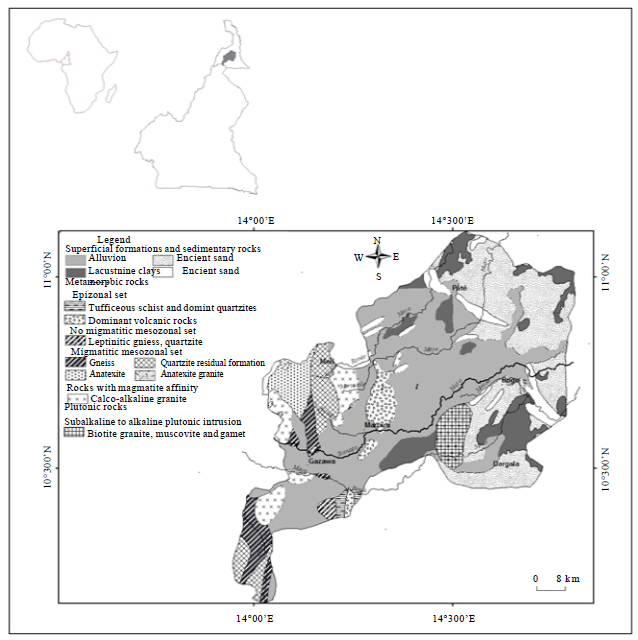
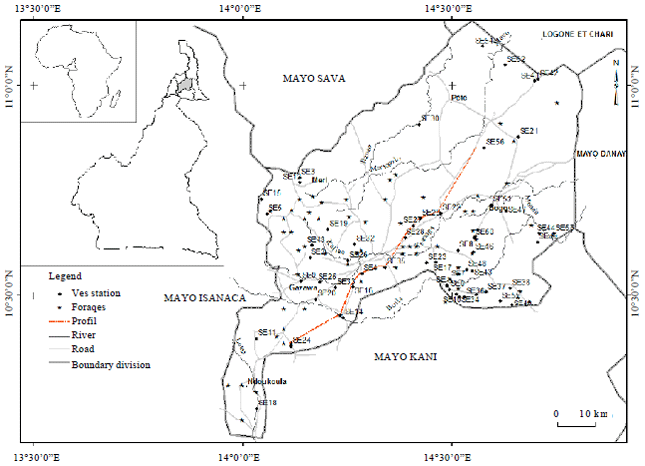
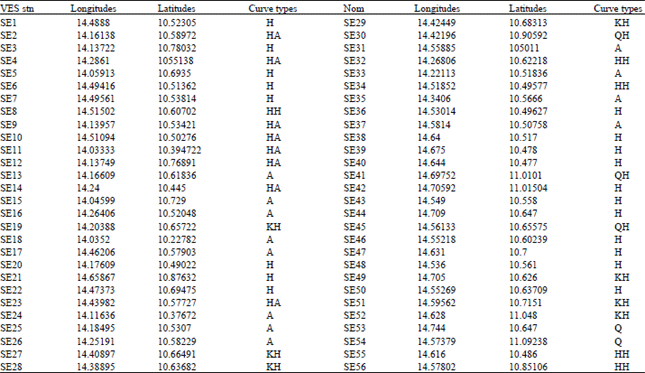
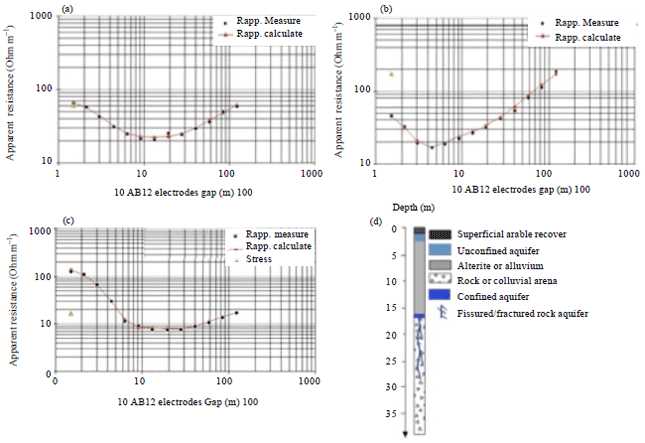
Research Article
Combined Use of Electrical and Flow Parameters for Hydrogeological Characterization of Piedmont Aquifers in the Basement Complex
Unit of Formation and Doctoral Research Geosciences and Applications, University of Yaounde I, P.O. Box 812, Yaounde, Cameroun
Philippe Njandjock Nouck
Unit of Formation and Doctoral Research Physics and Applications, University of Yaounde I, P.O. Box 812, Yaounde, Cameroun
Joseph Quentin Yene Atangana
Unit of Formation and Doctoral Research Geosciences and Applications, University of Yaounde I, P.O. Box 812, Yaounde, Cameroun
Joseph Mvondo Ondoua
Unit of Formation and Doctoral Research Geosciences and Applications, University of Yaounde I, P.O. Box 812, Yaounde, Cameroun