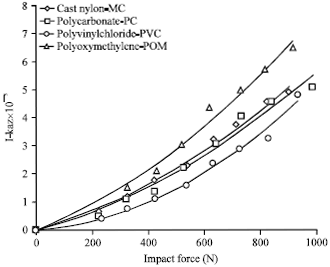
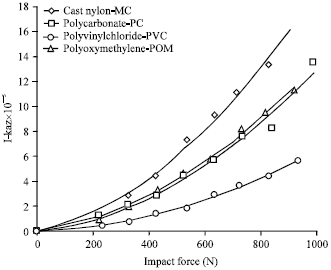
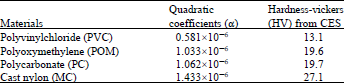
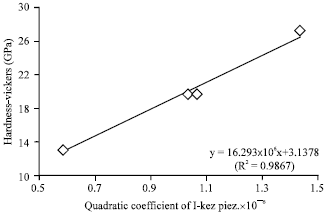
Research Article
Characterisation of Polymer Material Using I-Kaz™ Analysis Method under Impact Hammer Excitation Technique
Department of Mechanical and Materials Engineering, Faculty of Engineering and Built Environment,43600 UKM Bangi, Selangor, Malaysia
M.Z. Nuawi
Department of Mechanical and Materials Engineering, Faculty of Engineering and Built Environment,43600 UKM Bangi, Selangor, Malaysia
Mohammed T. Jasim
Department of Mechanical and Materials Engineering, Faculty of Engineering and Built Environment,43600 UKM Bangi, Selangor, Malaysia
A.R. Bahari
Faculty of Mechanical Engineering, UiTM (T) Kampus Bukit Besi,23200 Bukit Besi, Dungun, Terengganu, Malaysia
F.M. Nadia
Department of Mechanical and Materials Engineering, Faculty of Engineering and Built Environment,43600 UKM Bangi, Selangor, Malaysia