Research Article
The Weibull-Exponential Distribution: Its Properties and Applications
Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria
O.S. Balogun
Department of Statistics and Operations Research, Modibbo Adama University, Yola, Nigeria
H.I. Okagbue
Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria
S.A. Bishop
Department of Mathematics, Covenant University, Ota, Ogun State, Nigeria









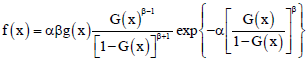
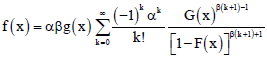
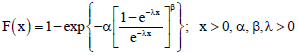
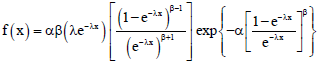
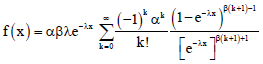

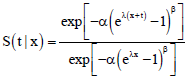
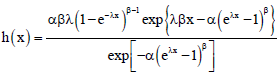
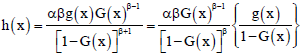
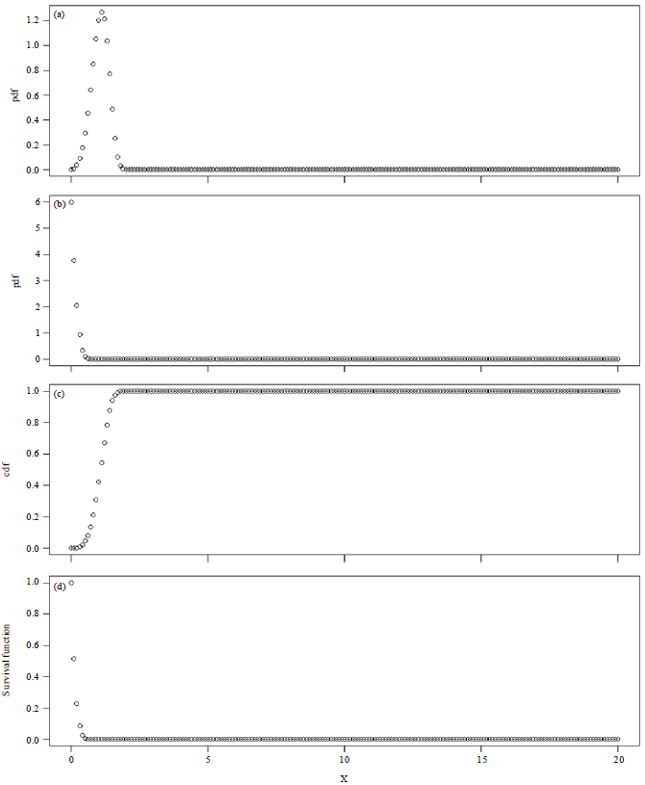
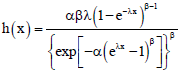
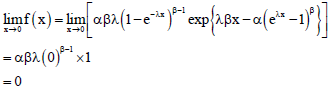
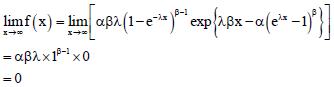
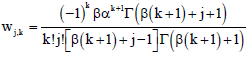
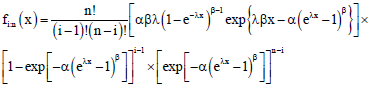

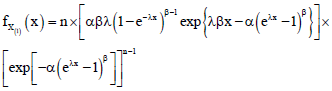
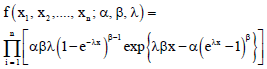


Fitri Yani Reply
I want to ask about Hazard function. Can I ask ******?