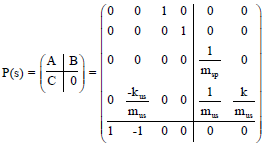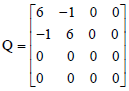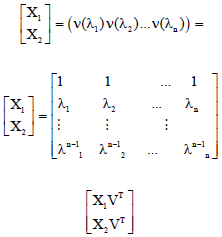Research Article
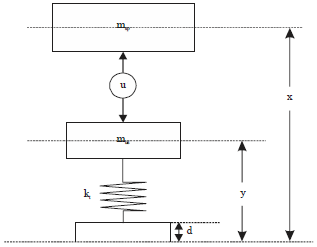
Symbolic Parametric LQR Controller Design for an Active Vehicle Suspension System
Centre for Automotive Research, Faculty of Engineering and the Built Environment, Universiti Kebangsaan Malaysia, 43600, UKM Bangi, Malaysia
Sallehuddin Mohamed Haris
Centre for Automotive Research, Faculty of Engineering and the Built Environment, Universiti Kebangsaan Malaysia, 43600, UKM Bangi, Malaysia
Zulkifli Mohd Nopiah
Fundamental Engineering Studies Unit, Faculty of Engineering and the Built Enviroment, Universiti Kebangsaan Malaysia, 43600, UKM Bangi, Malaysia