Research Article
Slope Stability Analysis Using Numerical Method
Department of Civil Engineering, College of Engineering, Diyala University, Diyala, Baghuba, Iraq
Generally a slope is a ground surface that positions at an angle to a horizontal level. Slopes may be creating from the natural or usually by people. Each slope has singular soil properties and geometric features which try to resist soil gravity or failure. Slope collapse cause the soil body to transfer downward and outward usually happening slowly or rapidly without attention. Slides generally start from hairline tension cracks which propagate inside the soil layers.
In Fact, numerous of studies had been exist since the manuscript of the earliest technique of analysis by (Huang et al., 2013) that were either related to slope stability or involved slope stability assessment issues. Among the existing approaches of analysis are the limit equilibrium methods of slices, boundary element methods (Jiang, 1990), finite element methods (Matsui and San, 1992) and neural network methods (Jaritngam et al., 2001). There are many other researches for the problem of slope issue using different method and especially FEM (Leong and Rahardjo, 2012; Li et al., 2009; Ji et al., 2012; Chai et al., 2013).
Thus, the slope stability problems need more and more studies. Usually, many researchers recommend to use finite element method for many reason. This useful and easy method can help the researchers and professionals to evaluate all expected issues can be developed during studying the problems of slope stability. Therefore, this study includes 2D finite element simulation and analysis of slope stability problems. Two types of soil as well as different slope angles have been used.
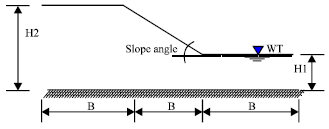 | |
| Fig. 1: | Profile view of slope stability problem |
Idealized model: Figure 1 shows plan and profile views of idealized prototype of side slope with width of 3B and height of H1 and H2. This project takes into account two types of soil, sandy and clayey soil. It has been assumed that the characteristics of these soils are constant during the study. In addition, the depth H1 is constant. While the study take various values of H2.
Analysis methodology and layout: A simple example with an idealized slope model is analyzed using most common Finite Element Method (FEM). In addition, the study compares the results from two types of soil. Finally, different parameters are studied to understand possible differences in computations of the Factor of Safety (FOS). The analysis consists of modeling of side slope by FEM using elasto-plastic model with 15-node triangular elements. The profile of side slope is with specified dimensions. The drained soil condition was used in this study which represents the case of dissipation of pore water pressure (i.e., the end of consolidation stage).
The baseline soil parameters used for the analysis of slope stability are illustrated in Table 1. Two type of soils were used in the analysis (i.e., cohesive and cohesion less soils).
| Table 1: | Soil parameters for analysis of slope stability group |
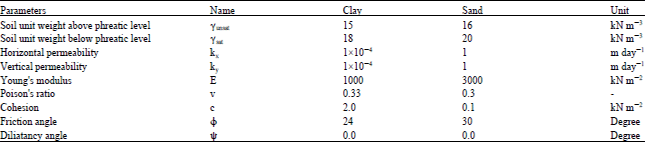 | |
 | |
| Fig. 2: | Two dimensional finite element mesh of side slope stability problem |
Finite element analyses were performed using the software PLAXIS 2D Foundation. In the finite element method a continuum is divided into a number of (volume) elements. Each element consists of a number of nodes. Each node has a number of degrees of freedom that correspond to discrete values of the unknowns in the boundary value problem to be solved.
The finite element mesh used in the simulation of single slope stability analysis (Fig. 2) consists of (1134) 15-nodes triangular element. Plan and 2D view for the finite element mesh of single slope stability and surrounded soil mass is illustrated in Fig. 2. The outer boundaries of soil body of are extended to 10 B on the sides and 5 B at the bottom of slope stability base.
Analyses were performed with several trail meshes with increasing mesh refinement until the displacement changes to very minimal with more refinement. The triangular elements used in the mesh are small and close to the slope stability body. All the nodes of the lateral boundaries (right and bottom) are restrained from moving in the normal direction to the respective surface.
In this part, the importance of conducting a fundamental study is established. A fundamental study is performed on the slope stability response by varying simulation parameter of the slope stability material (i.e., geometric dimension of the slope stability such as slope height H2). In addition, this part include, slope stability displacement where take into account the soil type which is very important to study that give the indication of the slope response at different site and geological characteristics.
This part includes the study of analysis of side slope stability (i.e., the collapse of the soil at the critical zone of the slope, safety analysis and displacement) under specific condition. Two type of soil used in the study (i.e., cohesive and cohesion less soil). B = 60 m, H2 = 1.5, 2, 2.5, 3 and 3.5 m. Influence of slope, soil parameters which include different cohesion intercept c' and Young modulus E for cohesive and cohesionless soil has been detailed in this section.
All results from the finite element program are included firstly the deformation mesh which is very important to study for all slope stability problems. This parameter is giving an indication the real slope deformation. However, this is can be used the check the weakness zone from the slope section. In addition, the results included the total displacement of the slope caused by geostatic stresses. As well as the total displacement direction which is important to estimate the direction of moving particles and which path is more risky compared with other parts. Finally, the results from the finite element program included the total and the effective stresses that are important to study for all geotechnical issues. Beside of that this study includes the factor of safety FOS for each case.
Slope analysis in cohesive soil: This part is includes the slope performance in clayey soil (i.e., Cohesive Soil). The properties of soil kept constant as well as all the dimensions of the whole problem. Only the high (H2) is changed, this change is represent in other hand the change in slope angle.
Figure 3a-e shows the results from finite element simulation of slope stability problem with H2 of 1.5 H1. It can be seems that the total displacement is small and the main deformation occurred at the toe of the slope as well as vertical displacement at the tip of the slope. This is possibly due to small amount of the interior stresses within soil mass which is results from small slope angle. In addition, it can see that the direction of the displacement take the shape of normal slope failure. Finally it can be seems that the effect of shape angle and soil type on both total and effective stresses is less influenced due to low soil stresses.
Figure 4a-e shows the additional results from Plaxis 2D for the simulation of slope stability problem for (H2 = 2.0 H1). This figure shows more influence of the slope angle on the slope performance.
Figure 5a-e shows the influence of slope angle on the slope stability problem with H2 of 2.5 H1. It can seems that the deformation mesh is largely influenced when increase of slope angle as well as the total and effective stresses.
Finally, Fig. 6 and 7a-e are include the results of high slope angle (i.e., H2 = 3.0 H1 and H2 = 3.5 H1). It can seems that these two angle provided little different in slope performance. This possibly due to the failure occurred at H2 = 3.0 H1) and not more or on the other hand can say that this angle gave high risk to fail and up to this value the risk still in maximum value.
Slope analysis in cohesionless soil: This part is includes the slope performance in sandy soil (Cohesionless Soil). As previous case, the properties of soil kept constant as well as all the dimensions of the whole problem. Only the high (H2) is changed, this change is represent in other hand the change in slope angle.
Figure 8a-e and as previous case it shows the results from finite element simulation of slope stability problem with H2 of 1.5H1. It can be seems that the total displacement is small and the main deformation occurred at the toe of the slope as well as vertical displacement at the tip of the slope. This is possibly due to small amount of the interior stresses within soil mass which is results from small slope angle. In addition, it can see that the direction of the displacement take the shape of normal slope failure. Finally it can be seems that the effect of shape angle and soil type on both total and effective stresses is less influenced due to low soil stresses.
Figure 9a-e and as previous case it shows the additional results from Plaxis 2D for the simulation of slope stability problem for (H2= 2.0 H1). This figure shows more influence of the slope angle on the slope performance.
Figure 10a-e and as previous case it shows the influence of slope angle on the slope stability problem with H2 of 2.5H1. It can seems that the deformation mesh is largely influenced when increase of slope angle as well as the total and effective stresses.
Finally, Figure 11 and 12a-e are include the results of high slope angle (i.e., H2 = 3.0 H1 and H2 = 3.5 H1). It can seems that these two angle gave little different in slope performance. This possibly due to the failure occurred at H2 = 3.0 H1) and not more or on the other hand can say that this angle gave high risk to fail and up to this value the risk still in maximum value and as previous case.
Development in total displacement: The total displacement is very important when study most of geotechnical problems. For this study, the total settlement which is measured with different slope angle can be seen in Fig. 13. This figure represents the total displacement verses the change in slope angle that measured by different H2. From this figure, it can be seems that the little or very small change in total displacement when small change in slope angle or small amount of H2. This is closed to the fact because of small stresses results from the slope body. While, it can be seems that the high influence of H2 (or slope angle) appeared when increase H2 up to 2.5H1. In addition it can be seems that the clayey soil is less resist compared with sandy soil especially at high slope angle.
Factor of safety: The factor of safety represents the main key for the analysis of slope stability problem. For both types of soil, the factor of safety increased when decreased the slope angle or H2. While, it can be seems that the slope angle for clayey soil provided relative high factor of safety (less risk) compared with the slope problem in sandy soil.
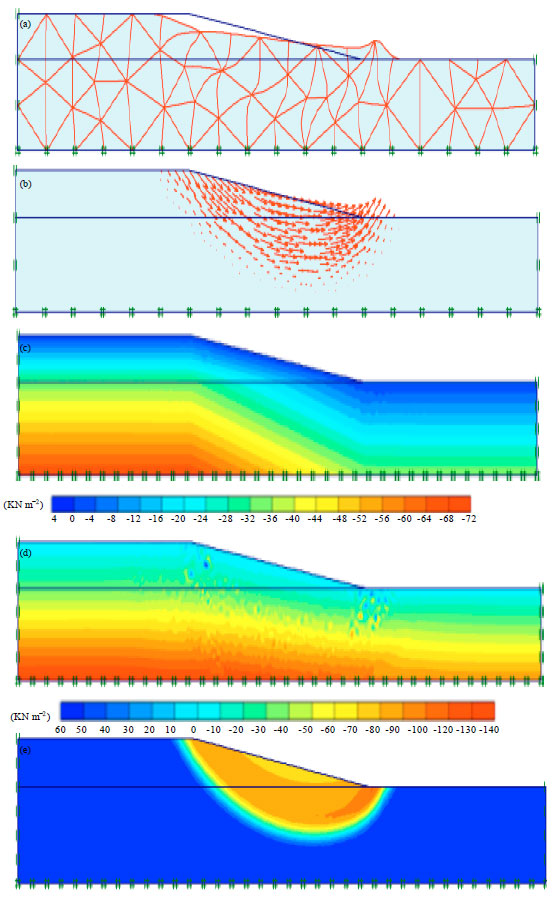 | |
| Fig. 3(a-e): | Results of slope stability analysis in clay for H2=1.5H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
 | |
| Fig. 4(a-e): | Results of slope stability analysis in clay for H2 = 2 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
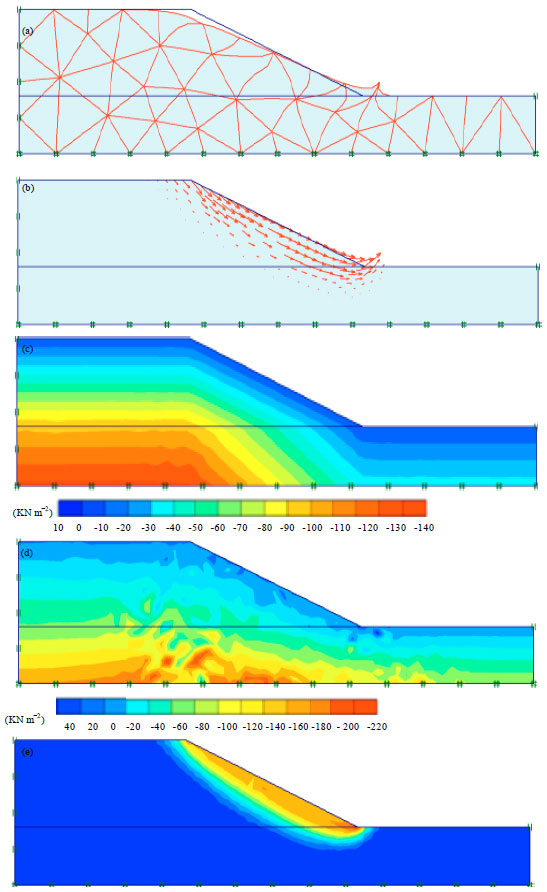 | |
| Fig. 5(a-e): | Results of slope stability analysis in clay for H2 = 2.5 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Total displacement, (d) Total stresses and (e) Effective stresses |
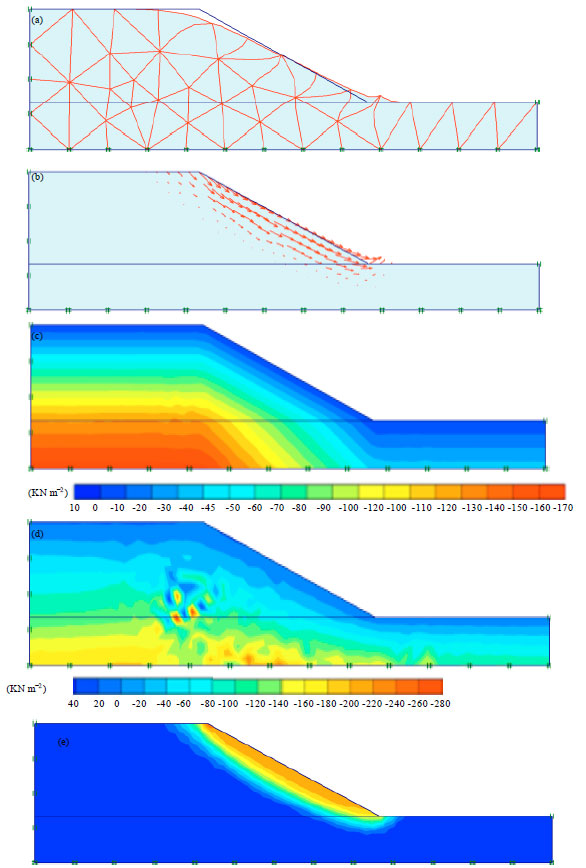 | |
| Fig. 6(a-e): | Results of slope stability analysis in clay for H2=3H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
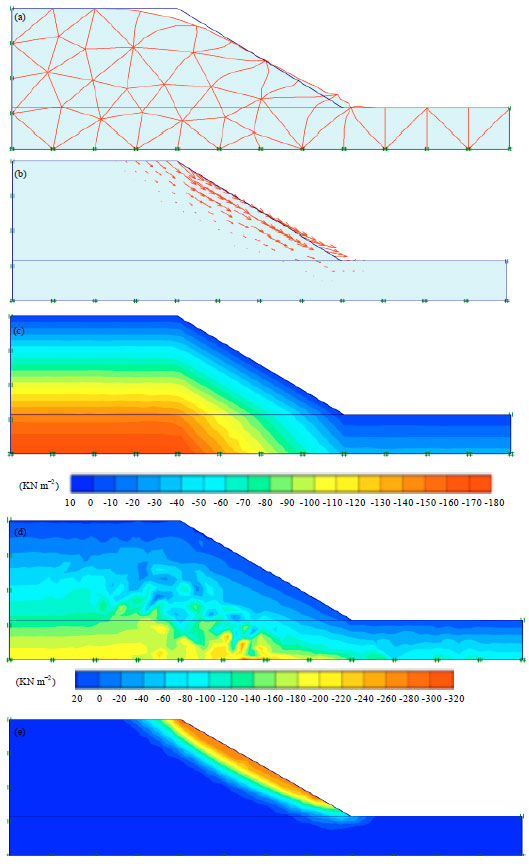 | |
| Fig. 7(a-e): | Results of slope stability analysis in clay for H2=3.5H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
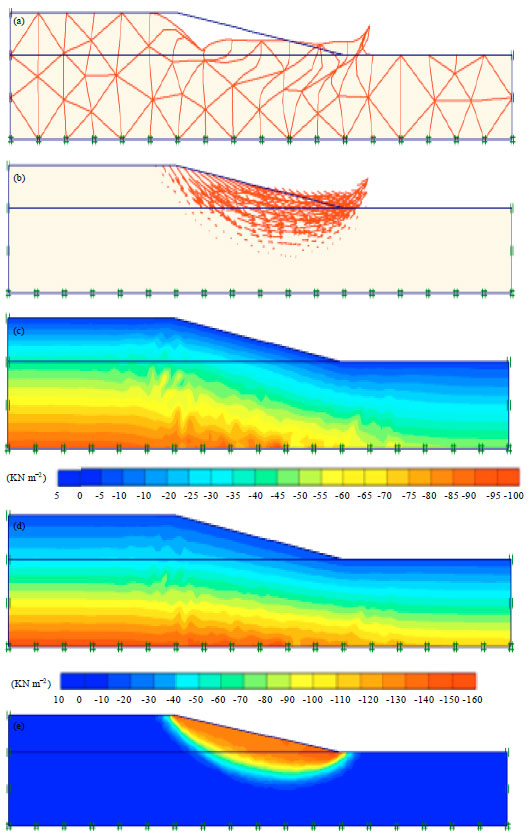 | |
| Fig. 8(a-e): | Results of slope stability analysis in sand for H2 = 1.5 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
 | |
| Fig. 9(a-e): | Results of slope stability analysis in sand for H2 = 2 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
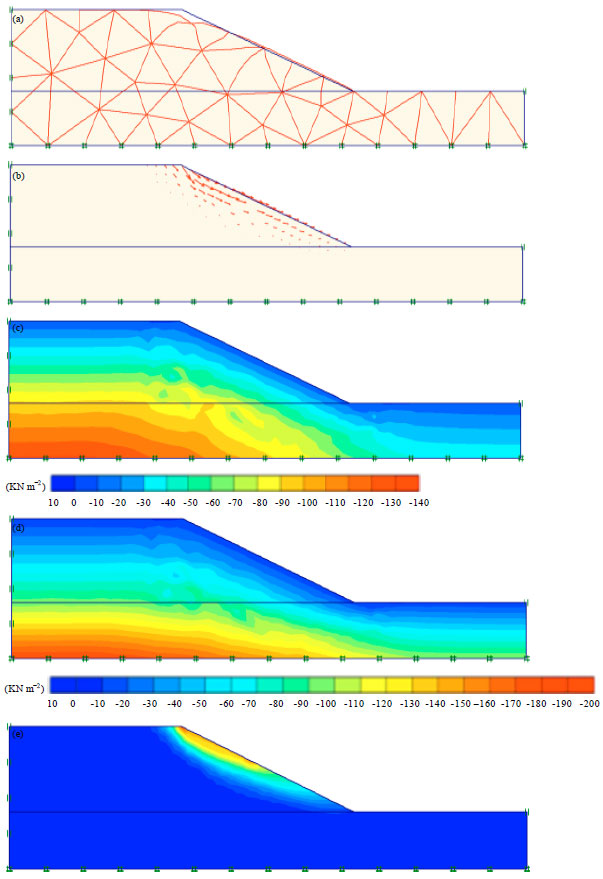 | |
| Fig. 10(a-e): | Results of slope stability analysis in sand for H2 = 2.5 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Effective stresses, (d) Total stresses and (e) Total displacement |
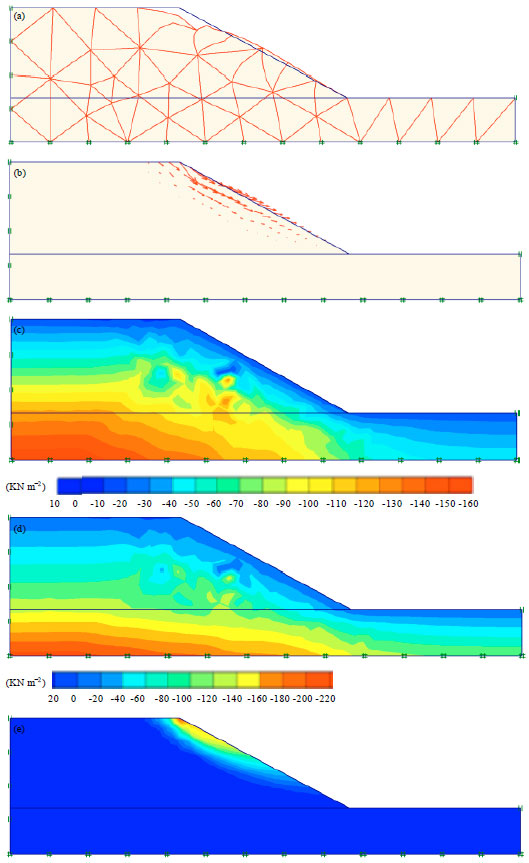 | |
| Fig. 11(a-e): | Results of slope stability analysis in sand for H2 = 3 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Total displacement, (d) Total stresses and (e) Effective stresses |
 | |
| Fig. 12(a-e): | Results of slope stability analysis in sand for H2 = 3.5 H1, (a) Deformation mesh, (b) Total displacement direction, (c) Total displacement, (d) Total stresses and (e) Effective stresses |
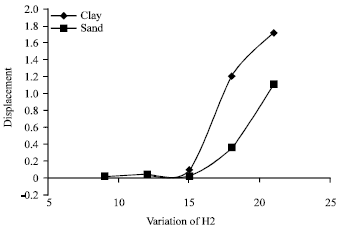 | |
| Fig. 13: | Relation between displacement and height in soil types |
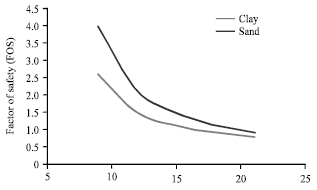 | |
| Fig. 14: | Factor of safety, clay and sand for different height in side slope structure |
| Table 2: | Factor of safety for clayey soil |
 | |
| Table 3: | Factor of safety for sandy soil |
 | |
Even the total displacement performance is revers as shown in Fig. 14 and Table 2 and 3. This is possibility due to the high soil resistance in case of clayey soil compared with sandy soil.
This part concludes the project with main findings from the assessment of slope stability performance. The main purpose of this project is to gain more information about the effect soil type and slope angle on the analysis of slope stability problems. The followings are conclusions obtained from this investigation:
| • | The slope performance is mainly influenced by the angle of slope as well as the types of soil |
| • | The main deformation occurred at the toe of the slope as well as vertical displacement at the tip of the slope |
| • | The direction of the displacement takes the shape of normal slope failure |
| • | The little or very small change in total displacement when small change in slope angle or small amount of H2 |
| • | High influence of H2 (or slope angle) appeared when increase H2 up to 2.5 H1 |
| • | The clayey soil is less resist compared with sandy soil especially at high slope angle |
| • | The factor of safety increased when decreased the slope angle or H2 |
| • | The slope angle for clayey soil gave relative high factor of safety (less risk) compared with the slope problem in sandy soil |