Short Communication
A Novel Evaluation Approach to University Extracurricular Sports Lifestyle based on ELECTRE-II
Department of Physical Education, Zhengzhou University of Light Industry, 450002, Zhengzhou, People`s Republic of China
In 1994, at the international meeting of Health Promotion and Physical Activity held by WHO and FIMS, the WHO presented the concept of sports lifestyle. In 1995, Japanese scholars once again proposed that the sports in the twenty-first century are a kind of cultural lifestyle, namely the sports lifestyle. Since, the Nationwide Fitness Program Outline was put into enforcement in 1995, the mass sports activities in China have entered a new stage of development and many scholars discussed the sports lifestyle, as well as the relation between lifestyle and sports from different angles (Arrow, 1963). The sports lifestyle is subject to the lifestyle system, being the part-whole relationship. It is the sum of sports activities and behavior characteristics for people to meet the requirements of self-maintenance and development by available sport resources according to their subjective desire under certain natural conditions and social background (Leyva-Lopez and Fernandez-Gonzalez, 2003). The sports lifestyle focuses on maintaining the exercise habit. The sports participative behavior is the most important manifestation of sports lifestyle which is also the key point to measure the sports lifestyles of different populations at various times.
The research object is the college students. Currently, the primary task of sports work in Chinese universities is to improve students’ health, the purpose of health education is to cultivate good health behavior and exercise habit for students, so that they can develop physically and mentally to enhance the social adaptation ability (Hwang and Masud, 1979). However, the PE once a week in universities can not satisfy the students to build up body and the problem that the physiques of college students in our country are declining can not be solved only by PEs. There are various factors influencing their physical health while the extra-curricular sports lifestyle is the most active and positive factor. The research on sports lifestyle evaluation indexes is to evaluate from physiology, psychology and sociology (Ngo and Mousseau, 2002). But since the college students have been during the course of physical education from primary school to university and their sports activities and physical training are of some regularity. Different from general population, their sports lifestyle has its own particularity. This study mainly studies the extra-curricular sports lifestyle of college students.
The research methods of this study can be summarized as follows:
| • | Literature method, consulting a large number of books and studys related to sports lifestyle both at home and abroad. Understand the concept, main features and contents of sports lifestyle. And list out the main contents of extra-curricular sports lifestyle on college students, including the purpose, site facility, project and effect of sports activities and up to basic standards of sport population, namely the time, frequency and intensity, respectively reach 30 min at a time, 3 times per week and above moderate intensity |
| • | The method of interview, consulting experts about the questionnaire contents and design plan, as well as the contents of extra-curricular sports lifestyle on college students |
| • | Questionnaire survey, developing the questionnaire according to above contents in five aspects, distributing 100 questionnaires and receiving 95 valid ones, with the valid return rate as 95% |
| • | Mathematical statistics, applying the SPSS 10.0 software to data reduction, statistics and comparison |
PERFORMANCE INDEX SYSTEM
After the evaluation objective is set, based on theoretical analysis, present the evaluation indexes determined initially. Design the questionnaire, whose contents are the purpose, site facility, project and effect of sports activities and up to basic standards of sport population, namely the time, frequency and intensity, respectively reach 30 min at a time, 3 times per week and above moderate intensity. It has a total of more than 30 questions. The reliability and validity test: The reliability coefficient R of this questionnaire is 0.87 and by expert judgment, its validity test shows that 80% experts agree with it. It can thus be seen that, this questionnaire has a good reliability and validity, meeting the requirements of statistics and research.
Consult the experts by Delphi method and request them to assign all the listed indexes by the five-grade scoring method. After the experts complete scoring, calculate the mean number to obtain the average score for each index and finally screen out the indexes with the average score ≥4. Count and optimize them (the second screening). Through experts’ evaluation and based on research need, the indexes were analyzed, respectively during the second screening. Then they were consolidated and concluded. The first-grade indexes are: The objectives of sports activities (fitness, entertainment, social intercourse); the sports activities process (site facility, sports event, sports time, frequency and intensity); the effects of sports activities (the results of fitness, education and social adjustment).
The retest method was employed to test their reliability. Firstly, test them two times and calculate the interclass correlation coefficients of their test results to obtain the test-retest reliability coefficients. The reliability coefficients between 0.65-0.75 are acceptable, fairly good between 0.75-0.85 and very good above 0.85, representing the degree of reliability for the tested indexes. The test results show that, the reliability coefficients of all indexes are within the acceptable range. The test project indexes are highly correlated to the sports lifestyle on college students. It indicates that the test indexes are highly associated with the extra-curricular sports lifestyle of college students. Therefore, this study will further analyze these indexes.
In an index system, the importance degrees of various indexes are different. In order to reflect their degrees of importance when making an evaluation conclusion, their corresponding weights should be determined. The weights of evaluation indexes in all grades can be determined by AHP method. (1) The experts sorted the evaluation indexes by their importance degrees in descending order through pair-wise comparison with their experiences and assigned relatively important rank values, (2) Construct matrixes to judge various index weight coefficients and (3) Calculate the weights q of all indexes to obtain the weight coefficients of the first and second grade indexes, as shown in Table 1. By testing the index weights, the reliability coefficient is 93% which is satisfactory.
PROPOSED APPROACH
In group decision, there are two ways to evaluate the alternatives, namely the consistency criterion and the respective evaluation. When the members in group decision committee can reach consensus on evaluation criteria and their weights, it can use the consistency criterion. If not, the respective evaluation should be used. Firstly each member should give the overall merits of alternatives and then collect their evaluations to form the group decision (Roy et al., 1986). Since, in the consistency criterion, the ELECTRE-II is used just once and the group sequencing could be obtained, this study employs the respective evaluation to solve the group decision problem.
The respective evaluation: When using this individual method, the attribute weights of criteria and alternatives applied by each member in the group can be different. Suppose that the union of criterion sets used by the decision maker i = 1,…, n is C = {c1, c2, …, ct}, its weight vector is Wi = (wi1, wi2,..., wip):
and wiq≥0, if the member i adopts the criterion p, wip = 0.
| Table 1: | Evaluation indexes and weights of extra curricular sports lifestyle on college students |
 | |
Following the steps of ELECTRE-II, we can get the individual ranking of alternatives by each decision maker in the group. After all the members sort the alternative sets, the ELECTRE-II method can be used to gather these individual rankings to form the group sequencing.
Firstly, suppose that the weight of the decision made by the decision maker i = 1,…, n in the group decision is wiε{w1, w2, …, wn} and the decision committee can obtain the weights of decision makers by the AHP method (Mayster et al., 1994). If the individual ranking of the member i shows that the alternative xk is better than the alternative xl (xkφi xl) and the set of all decision makers i satisfying the condition xkφi xl is written as I+(xk, xl), the set of members i satisfying the condition xk~ixl is I=(xk, xl) and the set of members i satisfying the condition xk~xl is I¯(xk, xl). Calculate the harmony indexes:
| (1) |
| (2) |
Determine the high, medium and low thresholds α*, α0 and α¯, 0.5<α¯<α0<α*<1. Given d0i<d*i and define Dhi, Dmi and Dli. Define the strong outranking relation and the weak outranking relation:
| (3) |
| (4) |
The forward strong and weak relation graphs Gs and Gw of alternative sets were constructed by the outranking relations of all the alternatives obtained by the above equations.
Firstly, make sort ascending by the directive diagram, calculate the sort v’(xi) of each alternative and draw the ranking table. Then mirror the forward strong and weak relation graphs to get the sort descending diagram, calculate the order v0(xi) of alternatives’ sort descending by using the same method and draw the sort descending table. Combined with the results of sort ascending and sort descending, by the equations:
| (5) |
v(xj) = 1+v*-v0(xj) | (6) |
| (7) |
Calculate the mean sort ![]() of alternatives and draw the mean ranking table of alternative sets and the group can get the final sort of alternative sets by the rule that the smaller the
of alternatives and draw the mean ranking table of alternative sets and the group can get the final sort of alternative sets by the rule that the smaller the ![]() is, the higher the rank of the alternative.
is, the higher the rank of the alternative.
RESULTS AND DISCUSSION
Taking the pratical decision problem as an example, we apply the respective evaluation to illustrate the above process and its reasonability. For ease of analytical calculation, suppose that an evaluation committee composed of p1, p2, p3, p4 and p5 evaluates x1, x2, x3, x4 and x5 in the alternative set X of three persons.
Individual decision: According to the criteria (the weight of attributes), the committee members sort all the persons by the ELECTRE-II:
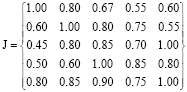
| Step 1: | Decision makerp1 gets the weighting of index attributes by the AHP method to reflect the relative importance of all attributes. The weight vector of the index system is set as w1 = {w11, w12, w13, w14, w15} = {0.1, 0.2, 0.25, 0.2, 0.25}. The pairwise comparison between persons according to the attribute yj(j = 1,…, 5) can obtain the set of all attributes yj satisfying the condition xk™jxl, the set J = (xk, xl) of all attributes yj satisfying the condition xk~jxl and the set J¯ = (xk, xl) of all attributes yj satisfying the condition xk™jxl: |
 |
Calculate the harmony indexes:
 |
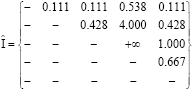 |
| Step 2: | A possible acceptable minimum value of resection is provided to each attribute by the connection method, namely only when each attribute value of an alternative is no lower than its corresponding value of resection, the alternative may be accepted, based on which the disharmony set Dj is constructed. Set the thresholds d*j = 0.5, d0j = 0.3, if yjk-yjl>dj, then the compensation of the other attributes is no longer accepted, namely xk™xl can not be admitted. Three disharmony sets Dhj, Dmj and Dlj can be defined according to the ‘Decision Theories and Methods’ |
| Step 3: | Given the high, medium and low thresholds of the harmony indexes, 0.5<α¯<α0<α*<1, in which α¯ = 0.6, α0 = 0.8 and α* = 0.9. Define the strong and weak outranking relations (Os and Ow) |
| Step 4: | Based on the above strong outranking relation Os and the weak outranking relation Ow, respectively draw the strong relation graph Gs and the weak relation graph Gw for the alternative set X |
| Step 5: | Make the sort ascending by the forward directive diagram and calculate the sort v’(xi) of all alternatives, as shown in Table 1 |
| The sort v’(xi) of all alternatives: |
 |
| Step 6: | Mirror the strong and weak relation graphs of sort ascending to get the sort descending diagram. Make the sort by the sort descending diagram, calculate the sort descending value v0(xi) of each alternative and list out the calculated values v(xi) of sort ascending and descending for each alternative, as shown in Table 2 |
Calculate the mean sort ![]() (xi) for each alternative as shown in Table 3. The sort of alternatives made by decision maker p1 is:
(xi) for each alternative as shown in Table 3. The sort of alternatives made by decision maker p1 is: ![]() The attribute weight given by the decision makers is:
The attribute weight given by the decision makers is:
 |
| Table 2: | Experimental results of v0(xi) and v(xi) |
Following the same steps can obtain the individual ranking of alternatives by the other members:
Group decision:
| Step 1: | Group determines the weight of each member by the AHP method as W = {0.3, 0.2, 0.25, 0.15, 0.1}. The individual ranking made by the decision maker i shows that the alternative xk is better than the alternative xl(xk™ixl). The set of all decision makers i satisfying the condition xk™ixl is written as I+(xk, xl), similarly, the set of members i satisfying the condition xk~ixl is i = (xk, xl) and the set of members i satisfying the condition xk™ixl is I¯(xk, xl). Calculate the harmony indexes and the experimental results can be listed as follows: |
 |
| Step 2: | Given the high, medium and low thresholds α*, α0 andα¯, 0.5<α¯<α0<α*<1; given d0i<d*i and define Dhi, Dmi and Dli. Define the strong and weak outranking relations based on which the strong relation graph GS and the weak relation graph GW are constructed |
| Step 3: | Make the sort ascending by the forward directive diagram and calculate the sort v’(xi) of all alternatives, as shown in Table 4 |
| Step 4: | Mirror the strong and weak relation graphs of sort ascending to get the sort descending diagram. Make the sort by the sort descending diagram, calculate the sort descending value v0(xi) of each alternative and list out the calculated values v(xi) of sort ascending and descending for each alternative as shown in Table 5 |
| Table 3: | Experimental results of |
| Table 4: | Experimental results of v’(xi) |
| Table 5: | Experimental results of v0(xi) and v(xi) |
| Table 6: | Experimental results of (xi) |
Calculate the mean sort ![]() (xi) for each alternative as shown in Table 6. Thus, the sort of alternatives made by the group is:
(xi) for each alternative as shown in Table 6. Thus, the sort of alternatives made by the group is: ![]()
The indexes were determined by the Delphi method. After expert surveys, the AHP was employed to analyze the results, obtaining the weights and sub-weights of all indexes. The grade evaluation criteria for indexes of extra-curricular sports lifestyle on college students were built by the percentile method. The extra-curricular sports lifestyle of 100 students in Wuhan University of Technology was tested by self-assessment and expert judgment make statistics of the results and compare them with the results from expert judgment. Upon testing, there is a significant relation between the evaluation result and the result of expert evaluation (p<0.01), indicating the consistency of the results obtained from these two evaluation methods is good.
The analysis of reliability and validity of evaluation results: The self-assessment reliability coefficient is 0.754, the expert evaluation reliability coefficient is 0.769, so the reliability is high and the evaluation results are reliable; the overall validity coefficient is 0.968, so the coefficient error is small and the validity is high. Thus, the evaluation index system of extra-curricular sports lifestyle on college students is of high reliability and validity.