Research Article
Scattering Sensitivity in Viscoelastic Composite with Multiple Delaminations
School of Science, Chang`an University, Xi`an, 710064, China
Deng Qing-Tian
School of Science, Chang`an University, Xi`an, 710064, China
Laminated composite plate-like structure has been increasing used in aircraft and aerospace industries due to their light weight and high strength. The failure of laminated composites under static or dynamic loadings could be mainly due to matrix cracking or delamination. Delamination may causes stiffness reduction and lead to the catastrophic failure of the structure which being the more severe of the two. The inspection of delamination is important to evaluate the reliability of the laminated composites. Even invisible delaminations could severely degrade the mechanical properties and loading capability of the laminas.
Lamb guided wave based method is very promising for structural health monitoring of composite materials which provide larger monitoring ranges, complete coverage of the waveguide cross-section, highly efficient and increased sensitivity to small defects. The problems of using Lamb waves are the infinite number of different modes that can propagation and all of the modes are dispersive. The basic factors for the selecting of Lamb wave mode and frequency may be enumerated as follows: (1) Dispersion; (2) Attenuation; (3) Sensitivity; (4) Excitability; (5) Detectability; (6) Selectivity (Wilcox et al., 2001).
Dispersion properties are important for mode identification and the knowledge of the mode attenuation helps maximizing the inspection range by exploiting modes associates to minimum attenuation. In the context of Lamb wave testing, attenuation may be defined as the reduction in signal amplitude with propagation distance. In most long range detection, the area of a structure which can be detected will be determined by the coefficients of attenuation of the chosen mode. Hence, the choosing of one effectively Lamb mode with lowest attenuation is considerable importance.
A Semi-analytical Finite Element (SAFE) method is utilized in the study to describe the Lamb wave propagation displacement field by coupling a finite element discretization of the waveguide cross-section with harmonic exponential functions along the wave propagation direction. Compared to other approaches, the SAFE method features: (1) Allows reducing of one order the numerical dimension of the problem; (2) Presents a wider spectrum of applicability; (3) Convenient for modeling waveguide with a large number of layers, e.g., composite laminates. Bartoli et al. (2006) applied SAFE method for modeling wave propagation in waveguides of arbitrary cross-section by accounting for material damping, including isotropic plates, anisotropic viscoelastic composite laminates, composite-to-composite adhesive joints and railroad tracks. Hayashi et al. (2005) discussed guided wave dispersion curves for a bar with arbitrary cross-section through theoretical analysis and experimental testing of rail Hayashi and Kawashima (2002) calculated the wave propagation in laminated plates with delaminations using the SAFE method and found that the reflections at delaminations occur not at the “Entrance” of delamination but at the “Exit”. Matt et al. (2005) investigated composite-to-composite joints representative of the wing skin-to-spar bonds of unmanned aerial vehicles by ultrasonic guided waves. Marzani et al. (2008) analyzed the wave propagation in viscoelastic axisymmetric waveguides by SAFE method. Shorter (2004) developed spectral finite element method and calculated the dispersion properties of wave propagation in linear viscoelastic laminates. Galan and Abascal (2005) studied bidimensional scattering problems of guided waves in laminated plates through the boundary element method in the frequency domain. Riccio and Tessitore (2005) analyzed the impact induced delamination in stiffened composite panels using an approach based on a threshold critical impact force. Yan and Yam (2004) studied damage detection of local and tiny delamination in a laminated composite plate using piezoelectric patches embedded in composite plate. Castaings and Hosten (2003) studied Lamb waves propagation in sandwich plates made of anisotropic and viscoelastic material layer by a semi-analytical model. Guo and Cawley (1993) discussed the interaction of the S0 Lamb mode with delamiantions in composite laminates by finite element analysis and experiment.
The present study investigated the sensitivity of different Lamb mode waves interaction with multiple delaminations in composite laminates by considering of material viscoelasticity. The Semi-analytical Finite Element (SAFE) method is utilized for modeling Lamb wave propagation in composite laminates and the material viscoelasticity is introduced by allowing complex stiffness matrix. The results indicated the degree of attenuation of the first several modes and provided more effective way of delamination detection application in composite laminates.
VISCOELASTIC MODELS
Wave propagation in linear viscoelastic media can be modeled by substituting complex components in the material stiffness matrix. The real part corresponds to the energy storage in wave propagation and the imaginary part corresponds to the damping introduced by the material viscoelasticity:
| (1) |
where, C' contains the storage moduli and C'' contains the loss moduli, both are 6 by 6 matrices.
Two models, the hysteretic model and the Kelvin-Voigt model, are used in modeling material damping which are both well-established in ultrasonic NDE. In the hysteretic model, the complex component of the stiffness matrix C'' is independent of frequency and in the Kelvin-Voigt model, C'' is a linear function of frequency. The measurement of C'' at a given frequency f0 is provided as a 6x6 matrix η. These two models can be expressed as follow (Rose, 1999):
| (2) |
| (3) |
The hysteretic model was considered in the study to represent material damping. The imaginary component of the stiffness matrix is frequency independent as showed in Eq. 2. Therefore, the hysteretic stiffness matrix has to be determined only once for the entire frequency range examined.
MATERIAL PROPERTY IN EACH LAMINA
In order to study Lamb wave propagation, the elastic constants of all the layers must be expressed in the global coordinate system (x1, x2, x3). For a composite material, this can be achieved through the rotation of the stiffness matrix of each lamina:
| (4) |
where, Cθ is the complex stiffness matrix in the global direction of the laminate, C is the complex stiffness matrix in the individual lamina’s principle directions, R1 and R2 are the rotation matrices from the principle material directions to the global laminate directions.
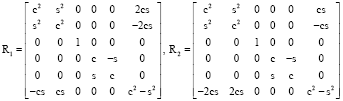 | (5) |
where c = cosθ and s = sinθ. Here, θ is the angle of rotation from lamina’s principle direction to the global direction and the value of θ is positive when the rotation is counterclockwise, as shown in Fig. 1.
 | |
| Fig. 1: | The relationship between principle direction and the global direction |
PROBLEM STATEMENT
Assuming wave propagates along direction x1 with wave number k and frequency ω. The cross section lies in the x2-x3 plane. The waveguide is composed of anisotropic viscoelastic materials. Lamb wave equations of motion are formulated by using Hamilton’s principle. And the variation of the Hamiltonian of the wave guide which vanish at all material points, is:
| (6) |
where, Φ is the strain energy and K is the kinetic energy. The strain energy is given by:
| (7) |
where, C is complex stiffness matrix, ε is stress field. The kinetic energy is given by:
| (8) |
where, ρ is the mass density, u is the displacement field.
By substituting Eq. 7 and 8 into Eq. 6, the Hamilton formulation can be rewritten as follow:
| (9) |
SAFE METHOD
A Semi-analytical Finite Element (SAFE) method simply requires the finite element discretization of the cross-section of the waveguide and the displacement along the wave propagation direction are conveniently described in an analytical fashion as harmonic exponential functions, thus reducing a 3-D problem to a 2-D one (Gao, 2006; Dong and Nelson, 1972). The general SAFE technique is extended to account for viscoelastic material damping by allowing for complex stiffness matrices for the material.
The plate section is discretized in the thickness direction x3 as showed in Fig. 2, where x3,1, x3,2, x3,3 are coordinates of nodes 1,2 and 3 along x3 direction, by a set of one-dimensional finite elements with quadratic shape functions and three nodes, with three degrees of freedom per node. The displacement vector can be approximated over the element domain as:
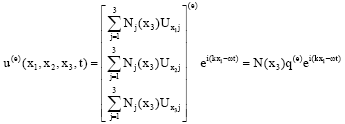 | (10) |
where, Nj(x3) is the shape functions:
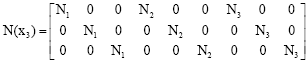 | (11) |
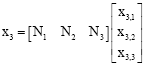 | (12) |
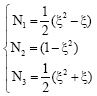 | (13) |
Ux1j, Ux1j, Ux3j, are the unknown nodal displacements in the x1, x2, x3 directions:
| (14) |
The strain vector in the element can be represented as a function of the nodal displacements:
| (15) |
 | |
| Fig. 2: | SAFE model of wave propagation in composite plate |
Where:
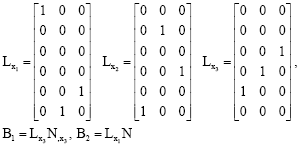 | (16) |
And:
By considering the total elements in the thickness, Hamilton formulation becomes to:
| (17) |
where, n is the total number of elements in the thickness direction and each elements represented a layer in the composite laminates in the study, ![]() and ρ(e) are the element’s complex stiffness matrix and mass density, respectively.
and ρ(e) are the element’s complex stiffness matrix and mass density, respectively.
By substituting Eq. 10 and 15 into Eq. 17 with some algebraic manipulation leads to:
| (18) |
Where:
 | (19) |
Applying standard finite element assembling procedures to Eq. 18:
| (20) |
where, U is the global vector of unknown nodal displacements:
| (21) |
Due to the arbitrariness of δU, the following wave equation is obtained:
| (22) |
Different from the wave propagation in an elastic media, the wave numbers k in the viscoelastic media obtained from Eq. 22 are generally complex, the real part ζ is related to the phase velocity of the wave mode and the imaginary part α is related to the attenuation. So, the wave number k can be expressed as:
| (23) |
For each wave number in Eq. 23, the final displacement solution of a Lamb wave mode can be expressed as follow:
| (24) |
SCATTERING SNESITIVITY
Two types of damage could occur in composite from guided wave point of view: one is introduced by long term environmental aging and fatigue, another type is delamination or damage introduced by mechanical impact appears as a discontinuity in material properties. In the latter case, wave scattering phenomenon can be used to detect the damage which will be discussed in this study. There are two dispersion curves are used to describe the guided waves in a viscoelastic medium: the phase velocity dispersion curve and the attenuation dispersion curve. Scattering sensitivity of guided Lamb wave is an important issue in damage detection and the quantitative analysis of Lamb wave scattering in composite plate with delamination is difficult. Auld (1990) presented an S-parameter method to indicate how much energy of the incident wave is converted into reflected waves and mode-converted transmission waves. S-parameter can be expressed numerically as:
| (25) |
where, v and σ are velocity and stress of the wave field in the composite plate in absence of delamination, v’ and σ’ are velocity and stress of the wave field in the composite plate in presence of delamination, SF is the surface of the delamination, ![]() is the direction normal at the surface of the delamination. The wave field in composite plate without delamination is considered to be the incident wave mode. In the presence of delamiantion, the damaged wave field can be approximated as stress free at the surface of the delamination (σ’ = 0). Then, Eq. 25 is simplified to the following:
is the direction normal at the surface of the delamination. The wave field in composite plate without delamination is considered to be the incident wave mode. In the presence of delamiantion, the damaged wave field can be approximated as stress free at the surface of the delamination (σ’ = 0). Then, Eq. 25 is simplified to the following:
| (26) |
Equation 26 indicated that the sensitivity is related to the stress distribution in the wave filed of the undamaged plate, the wave velocity of the damaged field at the boundary of the delamination and the shape of the delamination. However, the shape of the delamination and the wave field at the boundary of the delamination are difficult to obtain which are also case dependent, however, the sensitivity is directly related to the distribution of stress σ of incident wave at the position of the delamination from Eq. 26. In this study, the surface normal ![]() at the delamination is in the x3 direction.
at the delamination is in the x3 direction.
The following estimation of sensitivity of a guided Lamb wave mode for multiple delaminations with different propagation distances and depths with considering of material viscoelasticity and neglecting the detailed size of the delaminations, the sensitivity can be maximized by stress components (σ33, σ32, σ31):
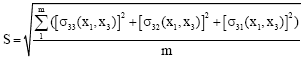 | (27) |
where, m is the number of delaminations, σ33(x1, x3), σ32(x1, x3), σ31(x1, x3) are the stress components at the position of delaminations by considering material viscoelasticity and their values can be calculated by substituting the obtained displacement fields from Eq. 24 into the constitutive relations:
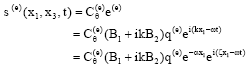 | (28) |
NUMERICAL RESULTS
Quasi-isotropic composite laminates are commonly used in aircraft structures, so a 8 layer quasi-isotropic composite is studied in the study. The thickness of the composite structure is 0.2 mm and the average layer thickness is 0.2 mm. Figure 3 shows a sketch of the lay-up sequence and the multiple delaminations in the composite. The x1 direction is in the fiber direction of the first layer, the fiber direction of the second layer is at θ = 45°, where θ can be found in Fig. 4. The plane wave propagation along the x1 direction is independent of x2, after rotated all the material properties into the (x1, x2, x3) coordinate system, phase velocity dispersion curve and attenuation dispersion curve can be calculated.
 | |
| Fig. 3: | The sketch of Lamb wave propagation in a 8 layers quasi-isotropic composite laminates [(0/45/90/45)] with multiple delaminations |
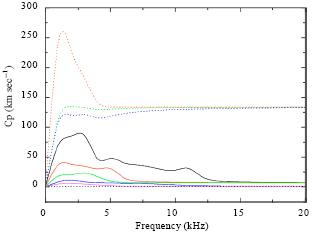 | |
| Fig. 4: | Phase velocity dispersion curve |
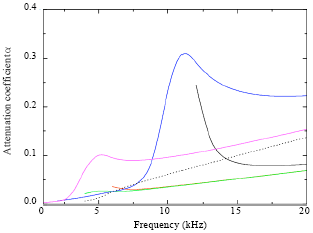 | |
| Fig. 5: | Attenuation dispersion curve |
The density is 1600 kg cm-3 (Neau et al., 2001). The viscosities are given at 2 MHz.
The material properties of the composite plate in the numerical simulation are shown in Table 1, Fig. 4 and 5 show the phase velocity dispersion curves and attenuation dispersion curves obtained from [(0/45/90/45)] laminates by considering hysteretic model. Figure 4 shows that with the increasing of frequency, the phase velocities of first several modes are trended to three values 133.453, 6.70315, 0.9518 km sec-1. From Fig. 5, it can be see that the major trend of attenuation increase with frequency but for some specific mode, the attenuation may decrease with increase of frequency. And the smallest attenuation can be found for a specific mode. Because only wave propagation in x1 positive direction is considered, the attenuation coefficient α is selected to be positive due to ![]() . So only positive values of α are illustrated in Fig. 5.
. So only positive values of α are illustrated in Fig. 5.
Figure 6-8 show sensitivity of first several modes for wave propagating in 0° direction of the laminates.
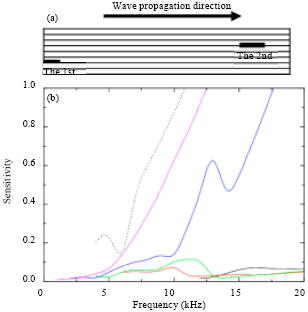 | |
| Fig. 6(a-b): | Sensitivity of different modes to two delaminations (the first between layer 2 and layer 3 the second between layer 5 and layer 6) (a) Location of two delamination and (b) sensitivity curve |
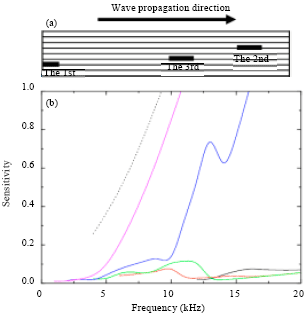 | |
| Fig. 7(a-b): | Sensitivity of different modes to three delaminations (the first between layer 2 and layer 3 the second between layer 5 and layer 6 the third between layer 3 and layer 4) (a) Location of three delamination and (b) Sensitivity curve |
In these cases, the delaminations are located at the first interface (between layer 2 and layer 3), the second interface (between layer 5 and layer 6), the third interface (between layer 3 and layer 4) and the fourth interface (between layer 7 and layer 8).
| Table 1: | The material properties of composite plate |
 | |
 | |
| Fig. 8(a-b): | Sensitivity of different modes to four delaminations (the first between layer 2 and layer 3; the second between layer 5 and layer 6 the third between layer 3 and layer 4 the fourth between layer 7 and layer 8) (a) Location of three delamination and (b) Sensitivity curve |
The first delamination is assumed located at the origin of the (x1, x2, x3) coordinate system, the distance between the first and the second delamination is 3 m, the distance between the first and the third delamination is 2 m and the distance between the first and the fourth delamination is 1 m. It can be see clearly that there existed three modes which sensitivities are higher than others and with consideration of attenuation from Fig. 5, the most available Lamb wave mode for delamination detection could be found through selecting suitable excitation frequency with higher sensitivity and lower attenuation.
In this study, sensitivity of the first several guided Lamb wave modes in viscoelastic composite laminates by considering multiple delaminations is studied. The semi-analytical finite element method is utilized for modeling wave in laminates and the material damping is introduced by using complex stiffness matrix. The hysteretic viscoelastic model is used and attenuation curves of wave amplitude are obtained. The numerical results of sensitivity of several modes are presented and provide some useful information for selecting more efficient Lamb wave mode in damage detection in composite laminates.
The Project was supported by the Special Fund for Basic Scientific Research of Central Colleges, Chang’an University.