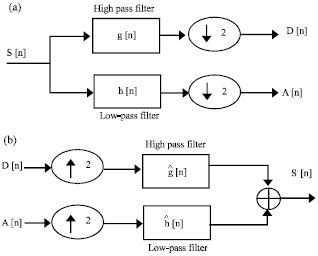
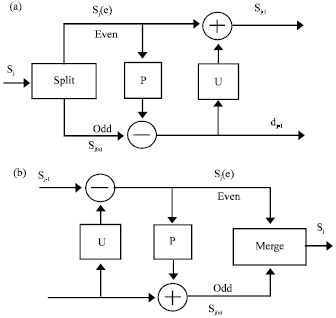
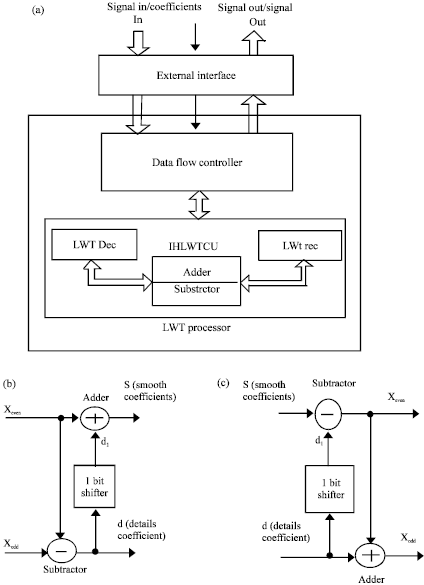
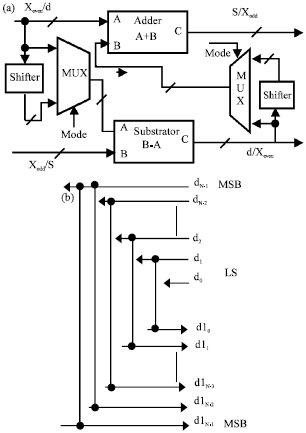
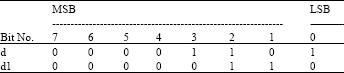
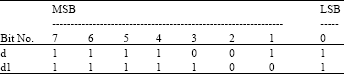
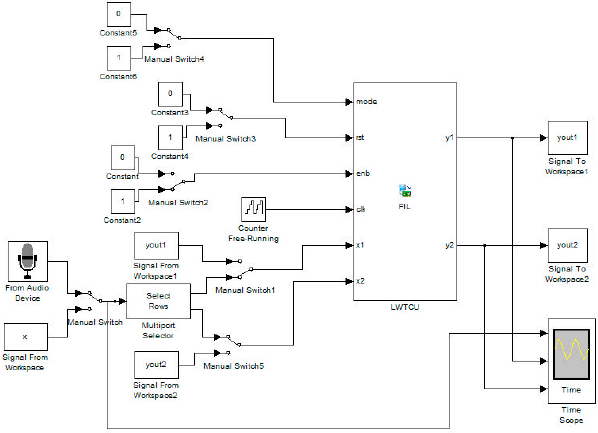
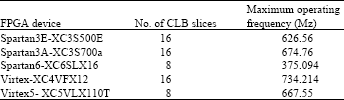Research Article
Efficient FPGA Architecture for Dual Mode Integer Haar Lifting Wavelet Transform Core
Department of Electrical Engineering, University of Babylon, Hila, Babil, Iraq
Razali Jidin
Electronic and Communication Engineering, Tenaga National University (UNITEN), Putrajaya, Malaysia
Wong Hung Way
Electronic and Communication Engineering, Tenaga National University (UNITEN), Putrajaya, Malaysia
Yassir Amer Abbas
Electronic and Communication Engineering, Tenaga National University (UNITEN), Putrajaya, Malaysia