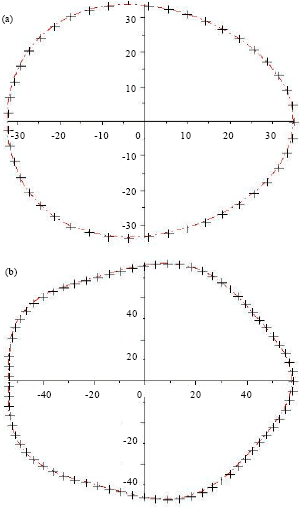
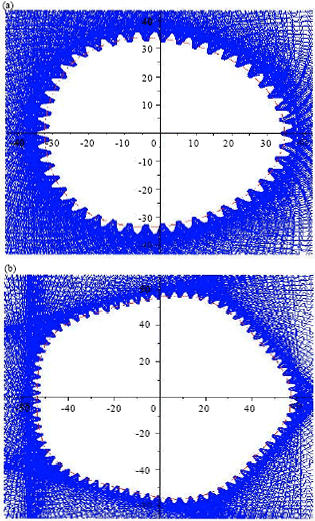
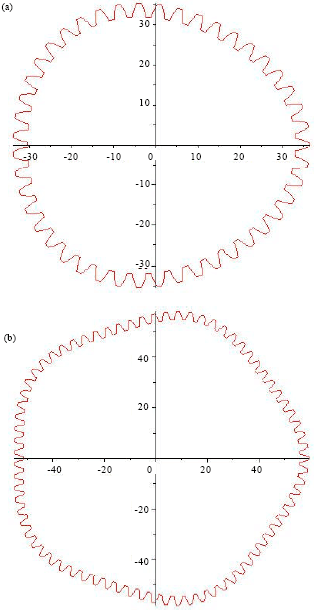
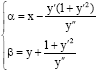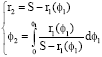Research Article
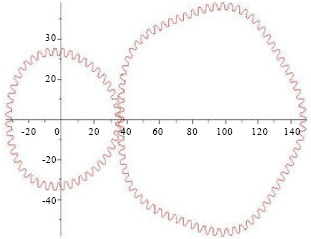
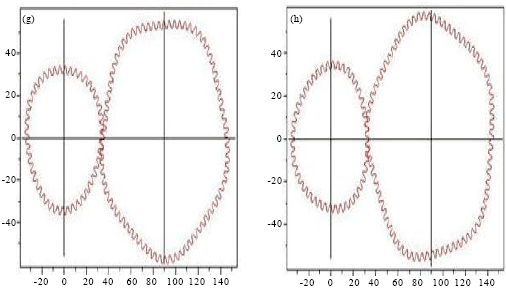
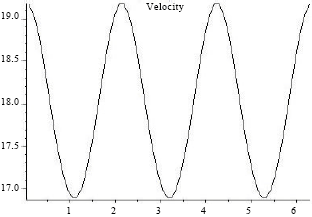
Tooth Profile Design and Kinematic Mechanism Simulation of Higher-order Elliptic Gears Based on MAPLE
Center for Engineering Teaching Practice, Tianjin Polytechnic University, 300387, Tianjin, China
Liu Jian
Center for Engineering Teaching Practice, Tianjin Polytechnic University, 300387, Tianjin, China