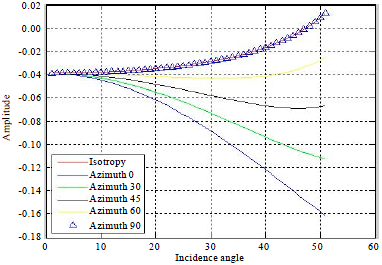
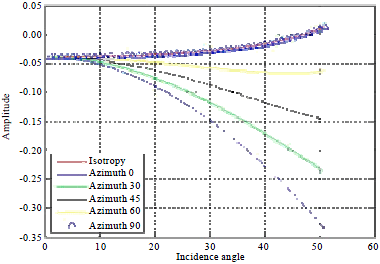
Research Article
Reflectivity of P-Wave Analysis for Fractured Reservoir Characterization in HTI Medium
Department of Petroleum Geosciences, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak Darul Ridzuan, Malaysia
Hilfan Khairy
Department of Petroleum Geosciences, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak Darul Ridzuan, Malaysia
T.H. Zuhar Zahir
Department of Petroleum Geosciences, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak Darul Ridzuan, Malaysia