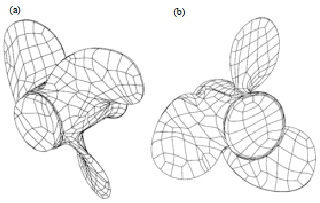
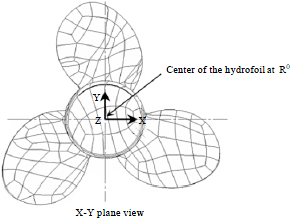
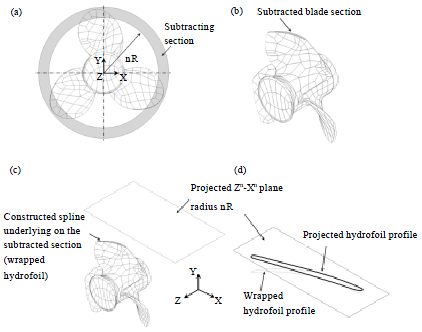
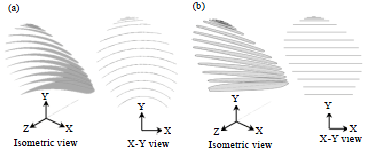
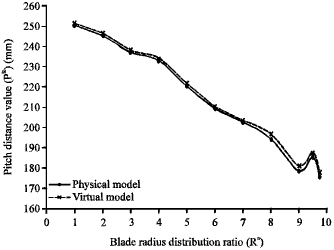
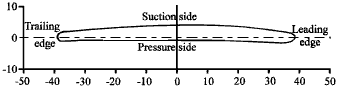
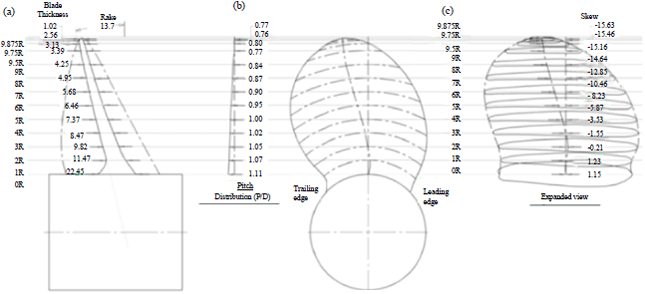
Research Article
Marine Propeller Geometry Characterization
Underwater Research Group, Materials and Minerals Unit, Faculty of Engineering, Universiti Malaysia Sabah, Jalan UMS, Kota Kinabalu, 88400, Sabah, Malaysia
Wai Heng Choong
Underwater Research Group, Materials and Minerals Unit, Faculty of Engineering, Universiti Malaysia Sabah, Jalan UMS, Kota Kinabalu, 88400, Sabah, Malaysia