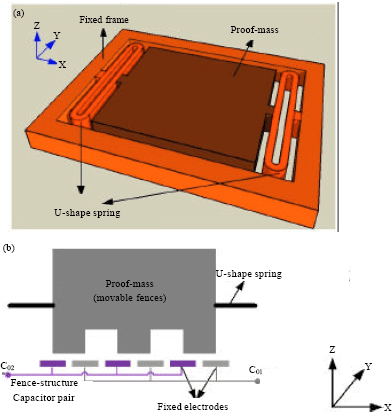
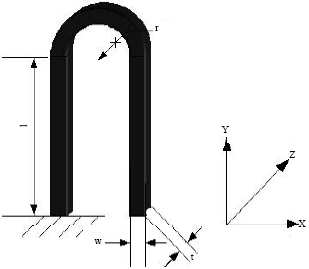
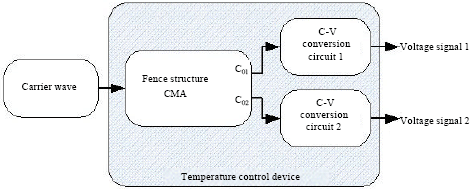
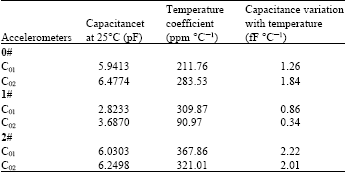
Research Article
Simulation and Optimization of Temperature Characteristic of Capacitive Micromachined Accelerometer System
Department of Electronic Engineering, Xi`an University of Posts and Telecommunications, Xi`an, 710121, People`s Republic of China