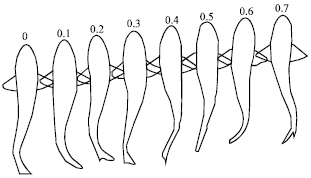
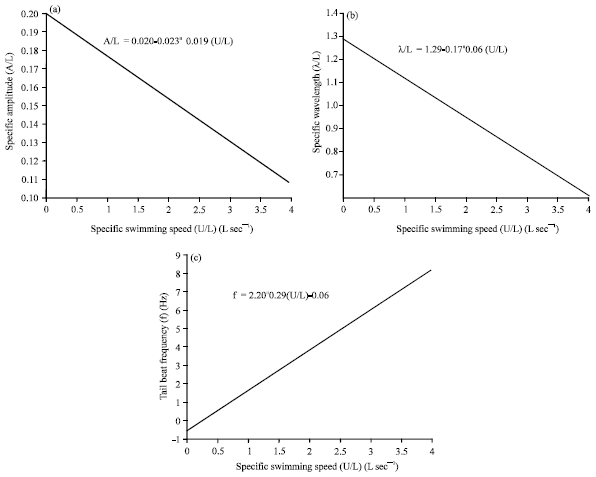
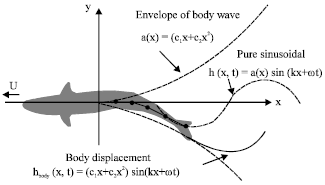
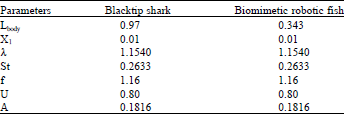
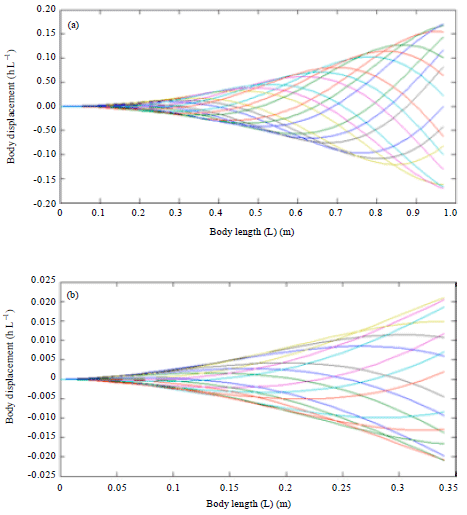
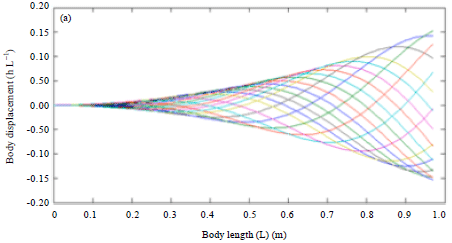
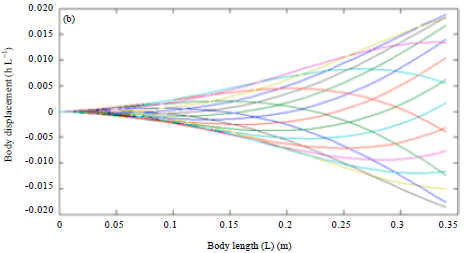
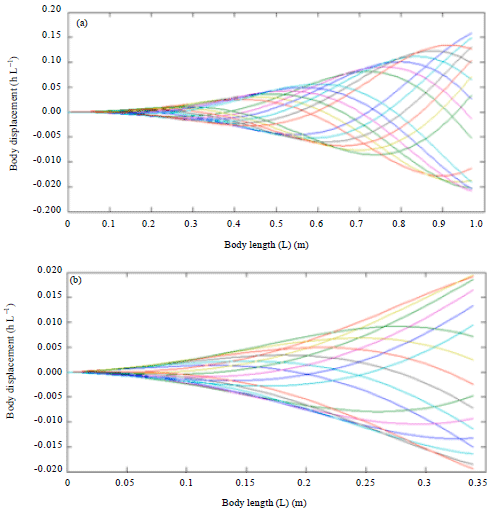
Research Article
Biomimetic Robot Fish Modelling Base on Shark Swimming Kinematics
Materials and Minerals Research Unit, Faculty of Engineering, Universiti Malaysia Sabah, Jalan UMS, Kota Kinabalu, 88400, Sabah, Malaysia
Wong Wei Loong
Materials and Minerals Research Unit, Faculty of Engineering, Universiti Malaysia Sabah, Jalan UMS, Kota Kinabalu, 88400, Sabah, Malaysia
Kenneth Tze Kin Teo
Materials and Minerals Research Unit, Faculty of Engineering, Universiti Malaysia Sabah, Jalan UMS, Kota Kinabalu, 88400, Sabah, Malaysia