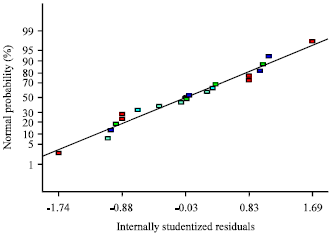
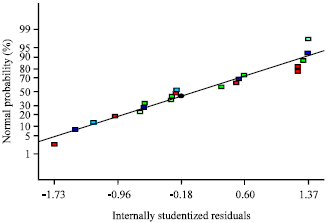
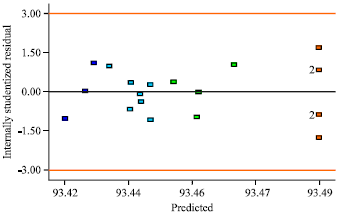
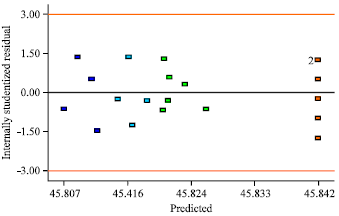
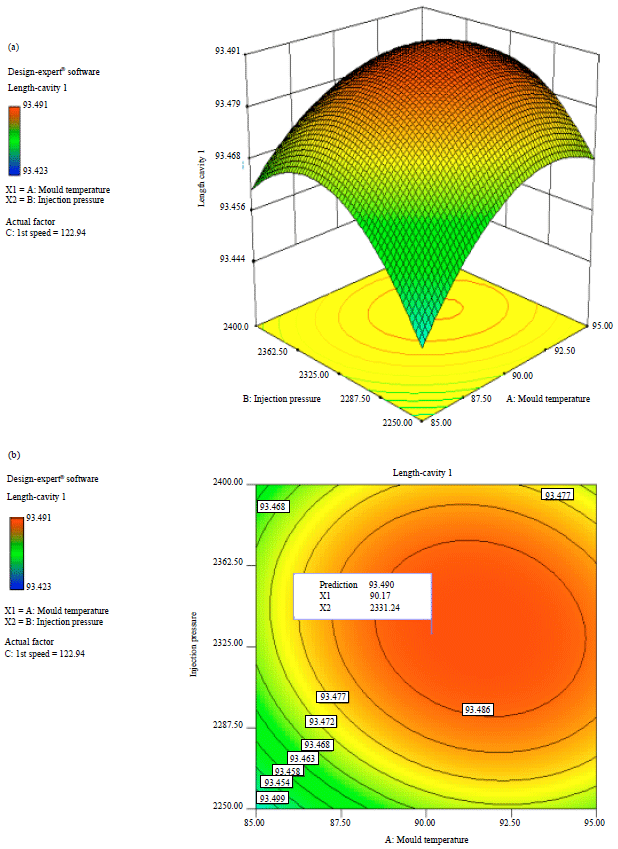
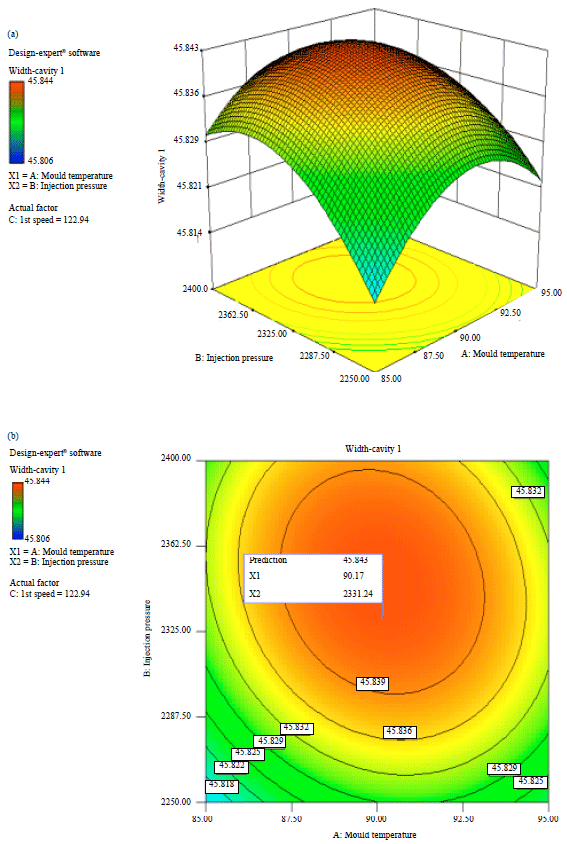
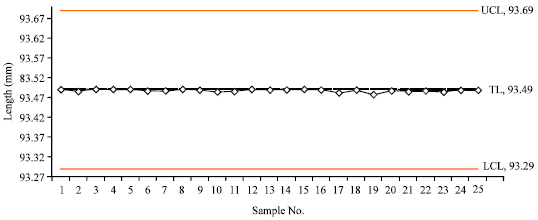
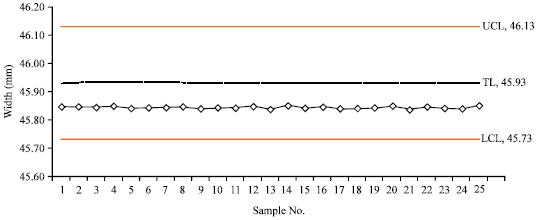
Research Article
Analysis of Optimal Injection Moulding Process Parameters for Thin-Shell Plastic Product Using Response Surface Methodology
Materials and Minerals Unit, Kota Kinabalu, Sabah, Malaysia
Jumat Sulaiman
Universiti Malaysia Sabah, Kota Kinabalu, Sabah, Malaysia
S. Rajalingam
Curtin University Sarawak, Miri, Sarawak, Malaysia