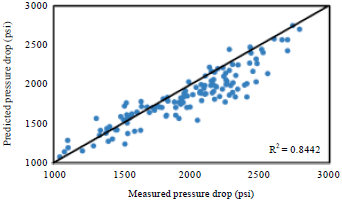
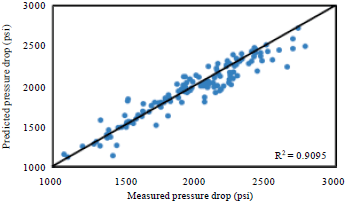
Research Article
A Comprehensive Study on the Current Pressure Drop Calculation in Multiphase Vertical Wells; Current Trends and Future Prospective
Department of Petroleum Engineering, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, Perak, 31750, Malaysia
Mohammed A. Ayoub
Department of Petroleum Engineering, Faculty of Geosciences and Petroleum Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, Perak, 31750, Malaysia