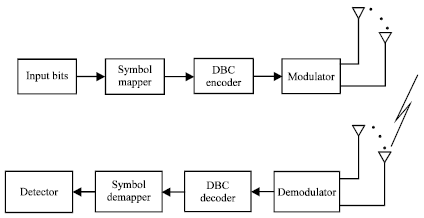
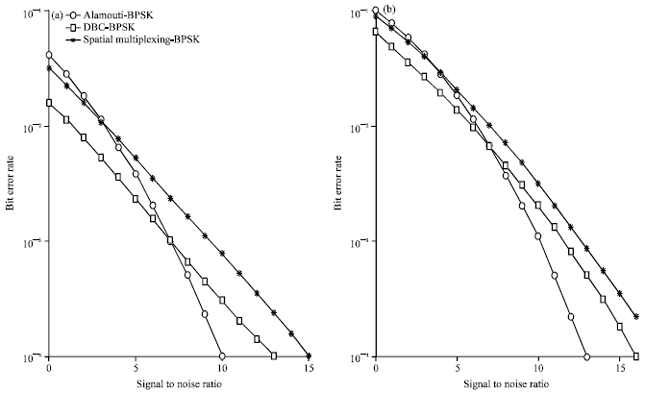
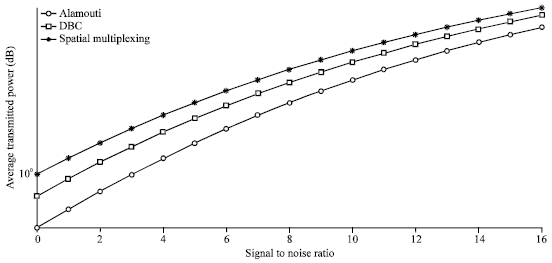
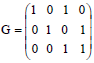Short Communication
Diversity Block Code: A Trade-off for Multiplexing and Diversity Gains
Faculty of Computing, Engineering and Sciences (FCES), Staffordshire University, Stafford, ST18 0AD, United Kingdom
Mohammad N. Patwary
Faculty of Computing, Engineering and Sciences (FCES), Staffordshire University, Stafford, ST18 0AD, United Kingdom
Abdel-Hamid Soliman
Faculty of Computing, Engineering and Sciences (FCES), Staffordshire University, Stafford, ST18 0AD, United Kingdom
Mohamed Abdel-Maguid
Division of Science and Technology, University Campus Suffolk (UCS), Ipswich, IP4 1QJ, United Kingdom