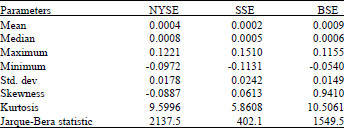
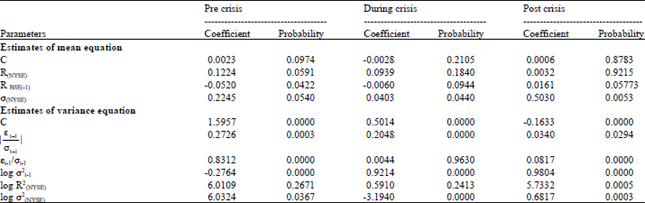
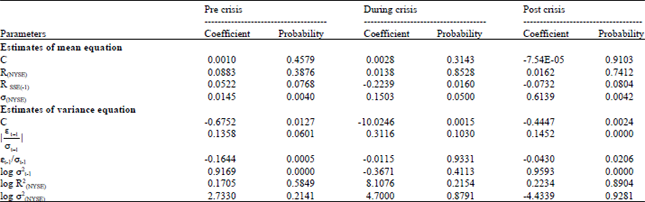
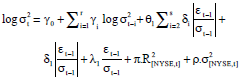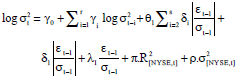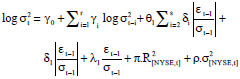Research Article
Global Financial Crisis: An EGARCH Approach to Examine the Spillover Effect on Emerging Financial Markets
School of Management, Harbin Institute of Technology, Harbin, 150001, China
Hui Xiaofeng
School of Management, Harbin Institute of Technology, Harbin, 150001, China
Saqib Gulzar
COMSATS Institute of Information Technology, Wah, Pakistan