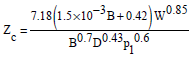Research Article
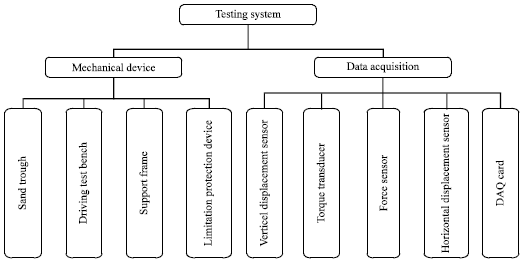
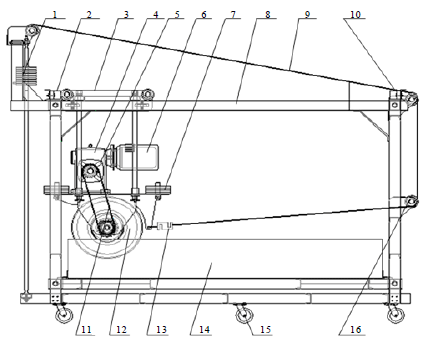
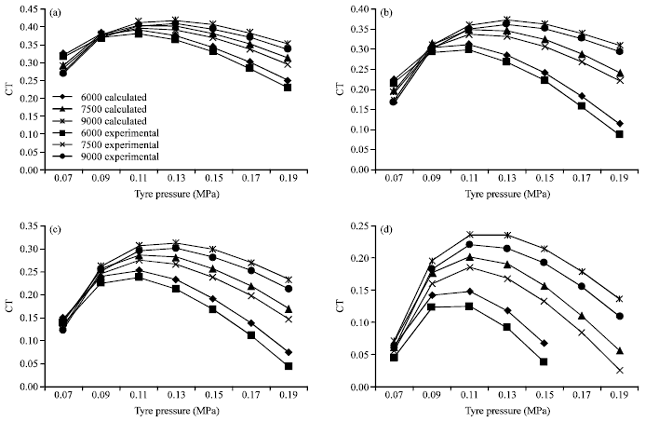
Relationship Between Tire Pressure and Tractive Characteristic of Beach Cleaner
School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen, Fujian, 361024, China
H. Wang
School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen, Fujian, 361024, China
Y. Tang
School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen, Fujian, 361024, China