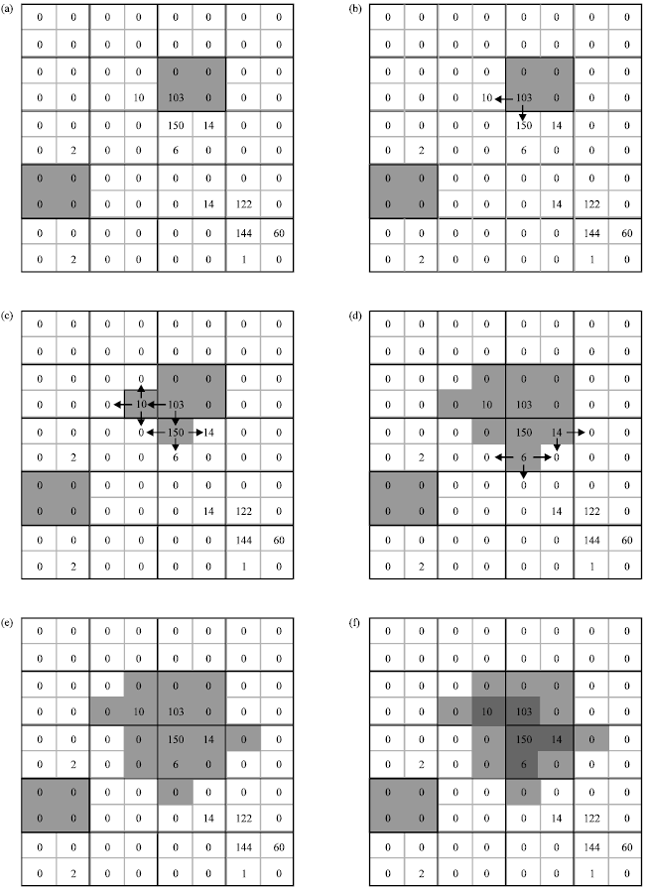
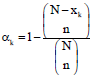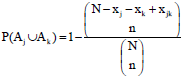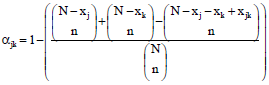Research Article
Adaptive Cluster Sampling with Spatially Clustered Secondary Units
Department of Statistics, Faculty of Science,Kasetsart University, Lat Yao, Chatuchak, Bangkok, 10900, Thailand
John J. Borkowski
Department of Mathematical Sciences, Montana State University,Bozeman, Montana, 59717, United States of America