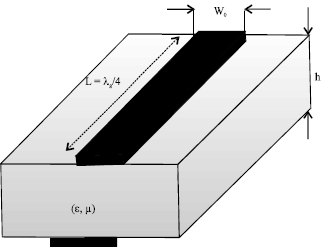
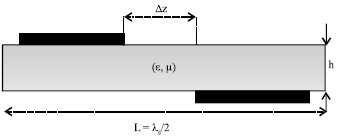
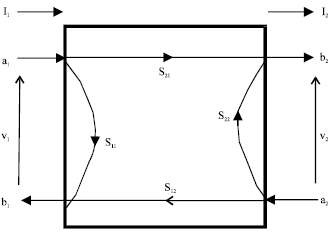
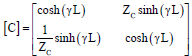Research Article
Electromagnetic Modelling and Design Principle of Parallel Plane Printed Microstrip Dipole Antennas
Groupe MOSE/Departement SEPT-ex SUPAERO, Toulouse, France
E. Tonye
Laboratoire d`Electronique et de Traitement du Signal-ENSP-UY 1, Yaounde, Cameroun
D. Bajon
Groupe MOSE/Departement SEPT-ex SUPAERO, Toulouse, France