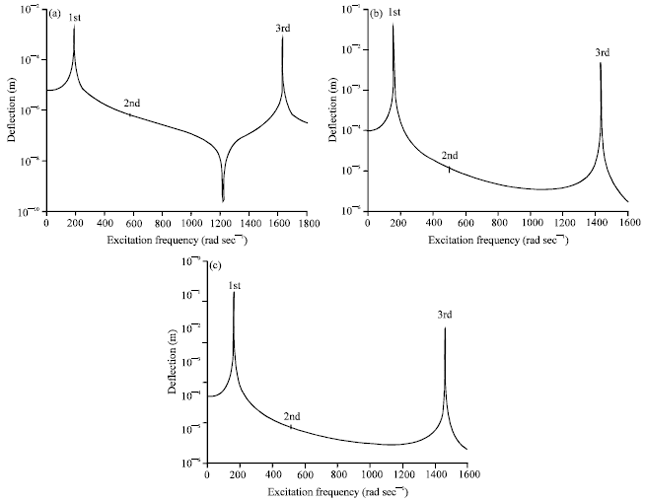
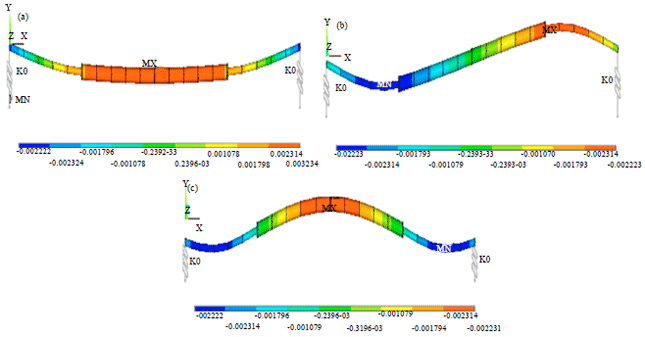
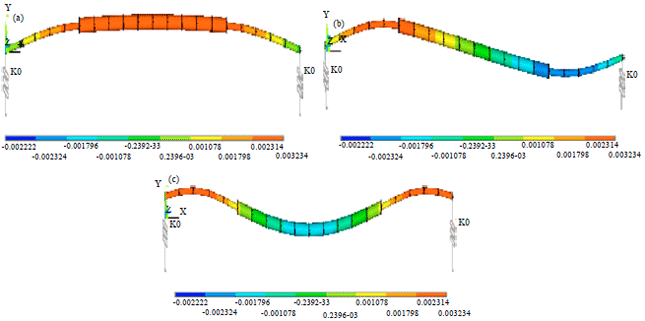
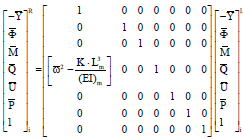Research Article
Effect of Various Fluid Densities on Vibration Characteristics in Variable Cross-section Pipes
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia
Hussain H. Al-Kayiem
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia
F. Hasan
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia
A.O. Mohmmedd
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia