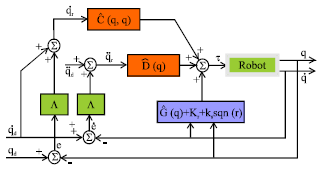
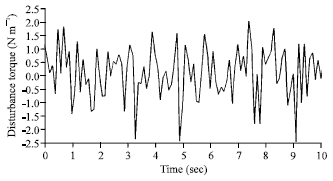
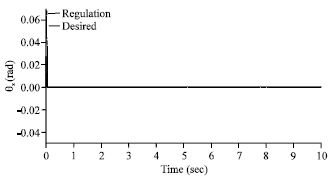
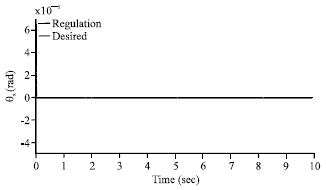
Research Article
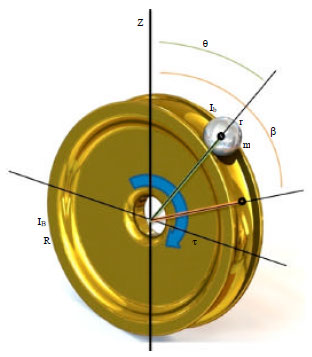
Control of a Ball on Sphere System with Adaptive Neural Network Method for Regulation Purpose
Young Researchers Club, Shiraz Branch, Islamic Azad University, Shiraz, Iran
Ehsan Zakeri
Young Researchers Club, Shiraz Branch, Islamic Azad University, Shiraz, Iran
Yousef Bazargan-Lari
Department of Mechanical Engineering, Shiraz Branch, Islamic Azad University, Shiraz, Iran
Mohammad Tavallaeinejad
School of Mechanical Engineering, Shiraz University, Shiraz, Iran