Short Communication
Multiple Linear Regression of Maximum Queue Length Probability Function for Infected Fish in the Fish Farms
Department of Mathematics, Faculty of Science, Port Said University, Port Said, Egypt
The maintenance of fish stock can be done through protecting it against diseases. Accordingly, the human health can be protected against infectious diseases transformed to him or her through the infected fish. Among the strategies of developing the fish resources at Egypt are fish farms constructing and exploring new areas of fish farms in areas where lands are not reclaimable. Among the common fish disease in fish farmed in Egypt are sleeping sickness, whirling, black spot and yellow grab. El Genidy (2011) has conducted study in queue system of maximal queue size with standard normal distribution for arrival times and this study was updated for providing the important relevant statistics in order to predict some related pieces of information in the future. Ekpenyong et al. (2008) improved the estimation based on sampling by using non linear regression method. Ismail et al. (2009) applied multiple linear regression method to predict the gold prices. Jin et al. (2006) carried out a method to estimate time traffic speed using multiple regression model. Okereke (2011a) has study the transformation on the parameter estimates of a simple linear regression model. Okereke (2011b) considered some consequences of adding a constant in the simple linear regression model. Subha and Stuwart (2010) performed multi resolution analysis in the texture classification using linear regression model. Yesmin et al. (2004) have done study infection in fish of swamps in Bangladesh. Naich et al. (2003) applied the kidney disease at fish farm on the river test. The results of this study will enable the researchers to deal with the amount of the infected fish in the farms with an economical manner and minimal costs.
DESCRIPTION OF THE PROBLEM AND ITS SOLVING
In this study, the distribution of inter-arrival times of infected fish follows the standard normal distribution. Let qn is the number of infected fish found in the fish farm, the sequence {qn} forms a discrete state Markov chain and the departure distribution is exponential with rate μ. In the queue system the probability of the maximum queue length depends on the following 3 independent events:
| A1 | = | Is the event that an infected fish arrived at time y, q0 = k, q1 = 0 and k = 0, 1,…, n given that y varies from 0 to t |
| A2 | = | Is the event that an infected fish at time y, q0 = k, q1 = k, q1 = k-l+1 and k = 0, 1…,n given that y varies from 0 to t |
| A3 | = | Is the event that no infected fish arrived during the time interval [0, t] = the event that the inter-arrival time is greater than t |
Then:
It is clear that:
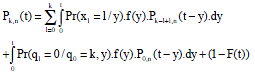 |
Where:
Then:
On the other hand:
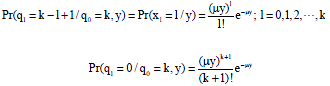 |
Therefore, when k = n the probability function of the maximum queue length during time (T = t) were obtained as follows:
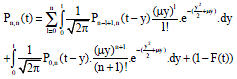 |
While:
Hence:
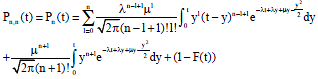 | (1) |
where, n is maximum queue length, λ is arrival rate, μ is departure rate, l is the number of departure units between 2 consecutive arrival units in the system and y is the time between consecutive arrivals.
Suppose that, arrival rate = λ = infected fish per unit time and departure rate = μ = 2 infected fish per unit time. Then by using mathematical program on Eq. 1, consequently Pn(t) was obtained as follows:
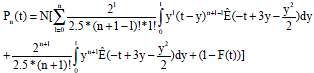 | (2) |
Equation 2 was converted to the formula of the multiple linear regression of the probability function of the maximum queue length Q infected fish during time T in days as a function in each random variables Q and T, where Q is a discrete random variable and T is a continuous random variable. Apply FIT command by using mathematical program on Eq. 2 as follows:
Fit[{{ti, q1, pq1(ti), {ti, q2, pq2(ti)},..., {ti, qm, pqm (ti)},
{t1, qj, pqj(t1)}, {t2, qj, pqj (t2)}, ..., {tr, qj, pqj(tr)},
(ti, qj, pqj (ti))},...,{tr, qm, pqm (tr)}}, {1, Q, T}, {Q, T}]
where, Q = q1, q2, q3,...,qm, T = t1, t2, t3,..., tr, i = 1, 2,..., r and j = 1, 2,..., m. Thus, for any given data of the random variables Q and T, the formula of the multiple linear regression of the probability function Z of the maximum queue length Q during time T were obtained in the form: Z = c-aQ-bT, where a, b, c are constant and c>0, a>0, b>0.
Corollary: If the probability function Z of the maximum queue length Q during time T as a function in each random variables Q and T takes the equation Z = c-aQ-bT, where c>0, a>0, b>0 are constant, q→0 and t→0 then z = c-aq-bt→c.
Lemma: If the probability function Z of the maximum queue length Q during time T as a function in each random variables Q and T takes the formula Z = c-aQ-bT, where c>0, a>0, b>0 are constant, then the cumulative distribution function F(Q, T) takes the Eq.:
Proof: The function:
was given then:
Therefore:
APPLICATION WITH NUMERICAL RESULTS
Ekpenyong et al. (2008) and El Genidy (2011) taken longer time in computation processes to find the information because there was not a program to implement.
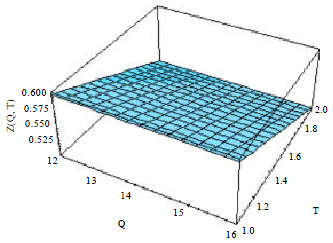 | |
| Fig. 1: | Multiple linear regression of infected fish in the fish farm |
The research by Ismail et al. (2009) and Jin et al. (2006) deal with multiple linear regression method without finding maximum queue length probability function. Okereke (2011a, b) and Subha and Stuwart (2010) performed a study in a simple linear regression model and it could not use in multiple linear regression model. Yesmin et al. (2004) and Naich et al. (2003) needed many procedures and computations to get the information. Method of finding information on infected fish in the fish farms in this study is more easy to get the necessary information because there was a program that could be applied to the computer, as well as the probability Z(Q, T) gives the degree of confidence for each result obtained.
Suppose the following data are given:
Q = q1, q2, q3, q4, q5 = 12, 13, 14, 15, 16 infected fish and
T = t1, t2 = 1,2 day, respectively.
By using the FIT command on the data, the following result was obtained:
Fit[{{1, 12, 0.6025}, {1, 13, 0.6025}, {1, 14, 0.6025},
{1, 15, 0.6025}, {1, 16, 0.6025}, {2, 12, 0.5115},
{2, 13, 0.5054}, {2, 14, 0.5051}, {2, 15, 0.5047},
{2, 16, 0.5046}}, {1, T, Q}, {T, Q}]
The last formula of Z(Q,T) gives an estimation for Pn(t), where ![]()
Figure 1 of Z (Q, T) was obtained by Plot3D command as follows:
Plot3D [Z, {Q, 12, 16}, {T, 1, 2}]
In Fig. 1, the multiple linear regression of infected fish in the fish farm was represented by the function Z(Q,T) such that the variable Q was represented by the maximum queue length of infected fish in the fish farm and the variable T was represented by the number of days.
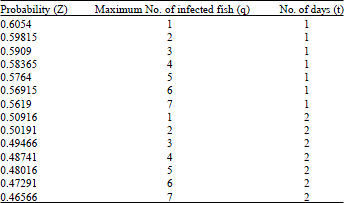
| Table 1: | Values of the probability Z with the maximum queue length q during time t |
 | |
There are some values of the variables T and Q which lead to Z(Q,T)<0 or Z(Q,T)>1, that is a contradiction, therefore all these values must be excluded. The following program solved this problem such that all the required values of T and Q satisfy the condition of the probability Z(Q,T).
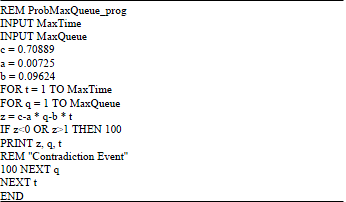 |
Suppose t = 1, 2 days and q = 1, 2, 3, 4, 5, 6, 7 maximum number of infected fish. After the implementation of the previous program, the following result was obtained.
In Table 1, some important information can be obtained such as, maximum number of infected fish q equals to one infected fish per one day with maximum probability Z = 0.6054, q = 7 infected fish per 2 days with minimum probability Z = 0.46566 and max q = 7 infected fish corresponds to Z = 0.5619 per one day and Z = 0.46566 per 2 days.
CONCLUSION
This study enables the researcher to find some of the required information such as, knowing the maximum time possible when the infected fish found in the fish farm or the maximum possible number of the infected fish that can be within the fish farm. Furthermore, the results of this study will enable the researchers to deal with the fish farms that contain infected fish in an economical manner and with minimal costs. Lastly, the idea of this study allows the researchers to apply it in various scientific fields.