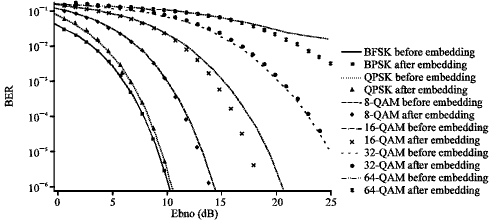
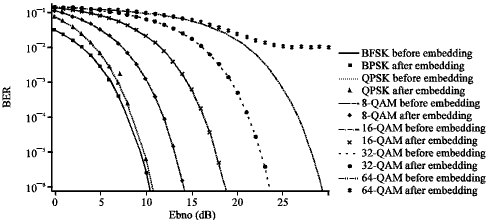
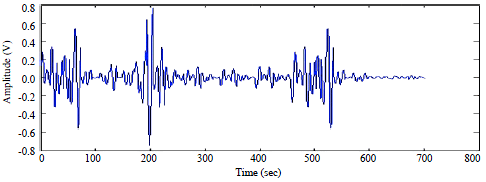
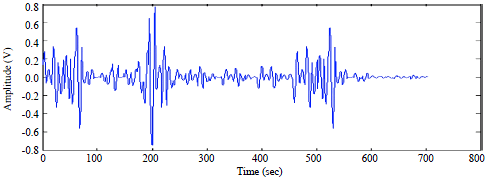
Research Article
Coded Crypted Converted Hiding (C3H)-A Stego Channel
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
Rengarajan Amirtharajan
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
K. Thenmozhi
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
J.B.B. Rayappan
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India