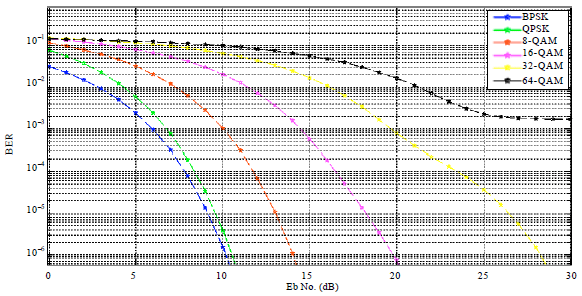
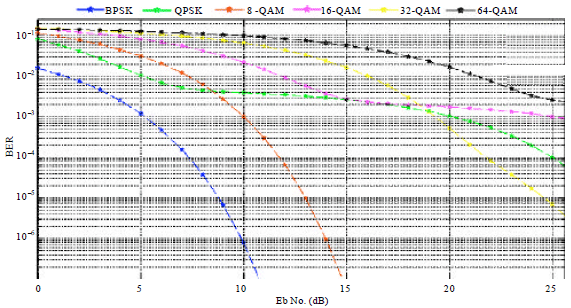
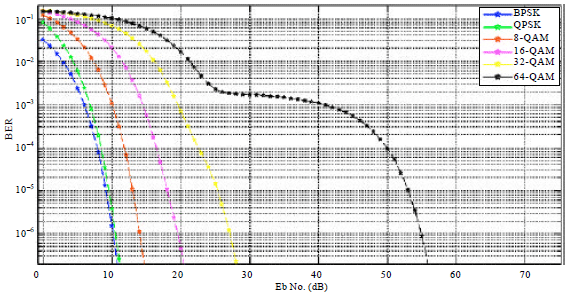
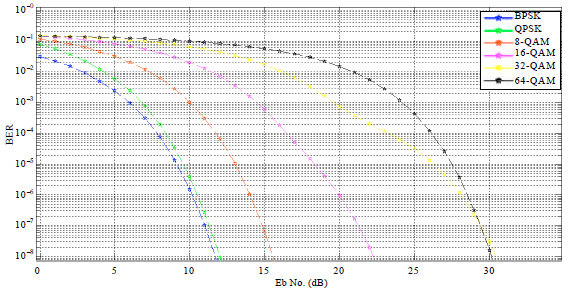
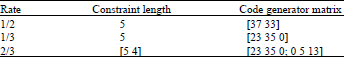Research Article
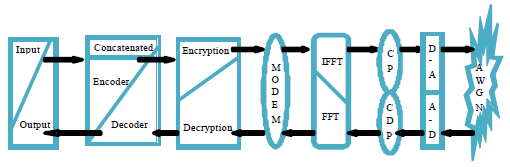
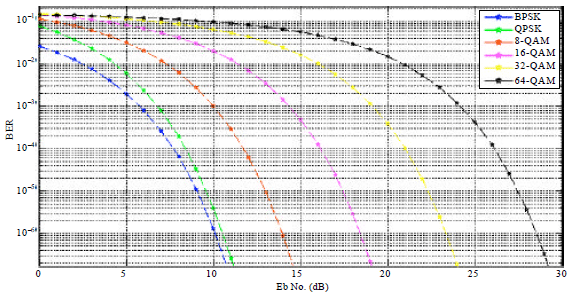
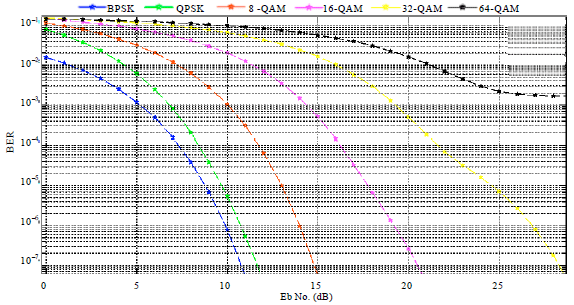
Double Layer Encoded Encrypted Data on Multicarrier Channel
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, Tamil Nadu, India
Rengarajan Amirtharajan
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, Tamil Nadu, India
K. Thenmozhi
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, Tamil Nadu, India
J.B.B. Rayappan
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, Tamil Nadu, India