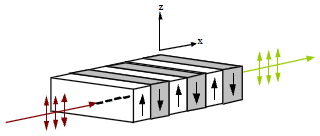
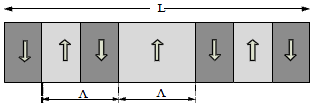
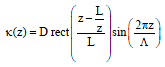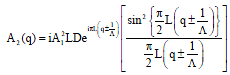Research Article
Fourier Analysis of Quasi-phase Matching Devices for WDM
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, India
Aravamudhan Mirunalini
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, India
Sundara Raman HariHara Subramani
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, India
Manohar ShyamKumar
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, India
Ragothaman K. Prasath
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, India
Shanmugam Boomadevi
Department of Physics, Periyar Maniammai University, Thanjavur, India
Krishnamoorthy Pandiyan
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, India